网址:http://m.1010jiajiao.com/timu_id_47211[举报]
一. 选择题(本大题共8小题,每小题5分,共40分)
题号
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
答案
A
B
A
D
D
B
C
C
二. 填空题(本大题共6小题,每小题5分.有两空的小题,第一空3分,第二空2分,共30分)
(9) .files\image229.gif) (10)
(10) .files\image231.gif) (11)
(11) .files\image233.gif) 或
或.files\image235.gif) (12)
(12) .files\image237.gif) (13)
(13) .files\image239.gif) ,
,.files\image241.gif)
(14) 10,
.files\image243.gif)
三.解答题 (本大题共6小题,共80分)
(15) (共12分)
解:(I).files\image245.gif)
.files\image129.gif) ,
,.files\image131.gif) ,
,
.files\image247.gif)
.files\image125.gif)
.files\image127.gif) =
=.files\image249.gif) ?
?.files\image251.gif)
.files\image253.gif) ------------------2分
------------------2分
.files\image255.gif) ------------------4分
------------------4分
.files\image256.gif)
.files\image135.gif) =
= .files\image258.gif) .
------------------5分
.
------------------5分
又.files\image137.gif)
.files\image261.gif)
.files\image263.gif) -----------------6分
-----------------6分
.files\image256.gif) 函数
函数.files\image137.gif) 的最大值为
的最大值为.files\image265.gif) .
------------------7分
.
------------------7分
当且仅当.files\image267.gif) (
(.files\image269.gif) Z)时,函数
Z)时,函数.files\image137.gif) 取得最大值为
取得最大值为.files\image265.gif) .
.
(II)由.files\image271.gif) (
(.files\image269.gif) Z),
------------------9分
Z),
------------------9分
得.files\image273.gif) ,
------------------11分
,
------------------11分
.files\image256.gif) 函数
函数.files\image137.gif) 的单调递增区间为[
的单调递增区间为[.files\image275.gif) ](
](.files\image269.gif) Z). ------------------12分
Z). ------------------12分
(16) (共14分)
解法一:
解:(Ⅰ).files\image278.gif) 且
且.files\image280.gif) 平面
平面.files\image282.gif) .--------------------2分
.--------------------2分
.files\image284.gif) 为
为.files\image286.gif) 在平面
在平面.files\image282.gif) 内的射影.
--------------------3分
内的射影.
--------------------3分
又.files\image289.gif) ⊥
⊥.files\image149.gif) , ∴
, ∴.files\image149.gif) ⊥
⊥.files\image147.gif) .
--------------------4分
.
--------------------4分
(Ⅱ) 由(Ⅰ).files\image149.gif) ⊥
⊥.files\image147.gif) ,又
,又.files\image149.gif) ⊥
⊥.files\image289.gif) ,
,
∴.files\image296.gif) 为所求二面角的平面角.
--------------------6分
为所求二面角的平面角.
--------------------6分
又∵.files\image298.gif) =
=.files\image300.gif)
.files\image149.gif) =4,
=4,
∴.files\image147.gif) =4 . ∵
=4 . ∵.files\image289.gif) =2 , ∴
=2 , ∴.files\image296.gif) =60°.
--------------------9分
=60°.
--------------------9分
.files\image302.gif) 即二面角
即二面角.files\image151.gif) 大小为60°.
大小为60°.
(Ⅲ)过.files\image304.gif) 作
作.files\image306.gif) 于D,连结
于D,连结.files\image308.gif) ,
,
由(Ⅱ)得平面.files\image310.gif) 平面
平面.files\image312.gif) ,又
,又.files\image314.gif)
.files\image316.gif) 平面
平面.files\image318.gif) ,
,
∴平面.files\image312.gif)
.files\image320.gif) 平面
平面.files\image318.gif) ,且平面
,且平面.files\image312.gif)
.files\image322.gif) 平面
平面.files\image324.gif) ,
,
∴.files\image326.gif) 平面
平面.files\image318.gif) .
.
∴.files\image328.gif) 为
为.files\image153.gif) 在平面
在平面.files\image318.gif) 内的射影.
内的射影.
.files\image331.gif) . -----------------11分
. -----------------11分
在.files\image333.gif) 中,
中,.files\image335.gif) ,
,
在.files\image337.gif) 中,
中,.files\image339.gif) ,
,.files\image341.gif) .
.
∴.files\image343.gif) =
=.files\image345.gif) .
-------------------13分
.
-------------------13分
所以直线.files\image347.gif) 与平面
与平面.files\image155.gif) 所成角的大小为
所成角的大小为.files\image349.gif) .
-------------------14分
.
-------------------14分
解法二:
解:(Ⅰ)由已知.files\image142.gif) ,
,
以.files\image062.gif) 点为原点,建立如图所示的空间直角坐标系
点为原点,建立如图所示的空间直角坐标系.files\image352.gif) .
.
则 .files\image354.gif) ,
,.files\image356.gif) .
-------------------2分
.
-------------------2分
则.files\image358.gif) ,
,.files\image360.gif) .
.
.files\image362.gif)
.files\image364.gif) .
.
.files\image366.gif) .
-------------------4分
.
-------------------4分
(Ⅱ).files\image368.gif) ,
,.files\image370.gif) 平面
平面.files\image282.gif) .
.
.files\image373.gif) 是平面
是平面.files\image282.gif) 的法向量. -------------------5分
的法向量. -------------------5分
设侧面.files\image318.gif) 的法向量为
的法向量为.files\image377.gif)
.files\image379.gif) ,
,
.files\image358.gif) ,
,.files\image360.gif) .
.
.files\image381.gif) ,
,
.files\image383.gif)
.files\image385.gif) .令
.令.files\image387.gif) 则
则.files\image389.gif) .
.
则得平面.files\image318.gif) 的一个法向量
的一个法向量.files\image377.gif)
.files\image392.gif) . -------------------7分
. -------------------7分
.files\image394.gif) .
-------------------8分
.
-------------------8分
即二面角.files\image151.gif) 大小为60°.
-------------------9分
大小为60°.
-------------------9分
(Ⅲ)由(II)可知.files\image377.gif)
.files\image392.gif) 是平面
是平面.files\image318.gif) 的一个法向量.
-------------------10分
的一个法向量.
-------------------10分
又.files\image399.gif) ,
, .files\image247.gif)
.files\image402.gif) .
-------------------13分
.
-------------------13分
所以直线.files\image153.gif) 与平面
与平面.files\image155.gif) 所成角为
所成角为.files\image406.gif) .
-------------------14分
.
-------------------14分
(17)(共13分)
解:(I)设乙闯关成功的概率为.files\image408.gif) ,丙闯关成功的概率为
,丙闯关成功的概率为.files\image410.gif) -------------------1分
-------------------1分
因为乙丙独立闯关,根据独立事件同时发生的概率公式得:
.files\image412.gif) -------------------3分
-------------------3分
解得.files\image414.gif) .
-------------------5分
.
-------------------5分
答:乙闯关成功的概率为.files\image416.gif) ,丙闯关成功的概率为
,丙闯关成功的概率为.files\image418.gif) .
.
(II)团体总分为4分,即甲、乙、丙三人中恰有2人过关,而另外一人没过关.
设“团体总分为4分”为事件A, -------------------6分
则.files\image420.gif) -------------------9分
-------------------9分
答:团体总分为4分的概率为.files\image422.gif) .
.
(III)团体总分不小于4分, 即团体总分为4分或6分,
设“团体总分不小于4分”为事件B, -------------------10分
由(II)知团体总分为4分的概率为.files\image422.gif) ,
,
团体总分为6分, 即3人都闯关成功的概率为.files\image424.gif) ------------------- 12分
------------------- 12分
所以参加复赛的概率为.files\image426.gif) =
=.files\image428.gif) -------------------13分
-------------------13分
答:该小组参加复赛的概率为.files\image430.gif) .
.
(18) (共13分)
解:(Ⅰ)第5行第5个数是29. ……………2分
(II) 由.files\image168.gif) 得
得.files\image433.gif) .
……………3分
.
……………3分
设.files\image435.gif) 是数列
是数列.files\image111.gif) 的前
的前.files\image437.gif) 项和, ∴
项和, ∴.files\image439.gif) .
.
当.files\image441.gif) 时,
时,.files\image443.gif) ……………5分
……………5分
当.files\image445.gif) 时,
时,.files\image447.gif) ……………6分
……………6分
又当.files\image441.gif) 时,
时,.files\image449.gif) ,
,
∴.files\image451.gif) ……………8分
……………8分
即数列.files\image111.gif) 的通项公式是
的通项公式是.files\image453.gif)
(III)由 (II)知数列.files\image111.gif) 是首项为1,公差为2的等差数列.
…………… 9分
是首项为1,公差为2的等差数列.
…………… 9分
∵前.files\image455.gif) 行共有项
行共有项.files\image457.gif)
∴第.files\image050.gif) 行的第一项为
行的第一项为.files\image460.gif) ………… 11分
………… 11分
∴第.files\image050.gif) 行构成首项为
行构成首项为.files\image463.gif) ,公差为2的等差数列,且有
,公差为2的等差数列,且有.files\image050.gif) 项.
项.
∴.files\image466.gif) .
……………13分
.
……………13分
(19)(共14分)
解:(I)设点.files\image468.gif) , 由已知得点
, 由已知得点.files\image191.gif) 在
在.files\image471.gif) 的中垂线上,
-------------------1分
的中垂线上,
-------------------1分
即.files\image473.gif) ,
------------------2分
,
------------------2分
根据抛物线的定义知,动点.files\image191.gif) 在以F为焦点,以直线m为准线的抛物线上, ------------------4分
在以F为焦点,以直线m为准线的抛物线上, ------------------4分
∴点
| ax2+bx+1 |
| cx+d |
| 2 |
(1)求f(x)的表达式;
(2)设g(x)=xf(x),正数数列{an}中,a1=1,an+12=g(an),求数列{an}的通项公式;
(3)设h(x)=
| 1 |
| 2 |
| 3 |
| 2x |
关于f(x)有如下命题:①f(-1)=0;②方程f(x)=0有无穷解;③f(x)有最小值,但无最大值;④f(x)的图象关于原点对称,且f(x)是周期函数.其中正确命题的序号是
 ,且当x>0时,f(x)有最小值
,且当x>0时,f(x)有最小值 ,又f(1)=3.
,又f(1)=3.(1)求f(x)的表达式;
(2)设g(x)=xf(x),正数数列{an}中,a1=1,an+12=g(an),求数列{an}的通项公式;
(3)设
 ,数列{bn}中b1=m(m>0),bn+1=h(bn)(n∈N*).是否存在常数m使bn•bn+1>0对任意n∈N*恒成立.若存在,求m的取值范围,若不存在,说明理由.
查看习题详情和答案>>
,数列{bn}中b1=m(m>0),bn+1=h(bn)(n∈N*).是否存在常数m使bn•bn+1>0对任意n∈N*恒成立.若存在,求m的取值范围,若不存在,说明理由.
查看习题详情和答案>>

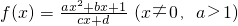 ,且当x>0时,f(x)有最小值
,且当x>0时,f(x)有最小值 ,又f(1)=3.
,又f(1)=3.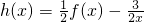 ,数列{bn}中b1=m(m>0),bn+1=h(bn)(n∈N*).是否存在常数m使bn•bn+1>0对任意n∈N*恒成立.若存在,求m的取值范围,若不存在,说明理由.
,数列{bn}中b1=m(m>0),bn+1=h(bn)(n∈N*).是否存在常数m使bn•bn+1>0对任意n∈N*恒成立.若存在,求m的取值范围,若不存在,说明理由.