题目内容
奇函数 ,且当x>0时,f(x)有最小值
,且当x>0时,f(x)有最小值 ,又f(1)=3.
,又f(1)=3.(1)求f(x)的表达式;
(2)设g(x)=xf(x),正数数列{an}中,a1=1,an+12=g(an),求数列{an}的通项公式;
(3)设
 ,数列{bn}中b1=m(m>0),bn+1=h(bn)(n∈N*).是否存在常数m使bn•bn+1>0对任意n∈N*恒成立.若存在,求m的取值范围,若不存在,说明理由.
,数列{bn}中b1=m(m>0),bn+1=h(bn)(n∈N*).是否存在常数m使bn•bn+1>0对任意n∈N*恒成立.若存在,求m的取值范围,若不存在,说明理由.
【答案】分析:(1)根据f(1)=3,以及f(x)为奇函数可求出b的值,然后根据当x>0时,f(x)有最小值 ,可求出c的值,从而求出函数的解析式;
,可求出c的值,从而求出函数的解析式;
(2)根据an+12=g(an)可证得{an2+1}为等比数列,其首项为a12+1=2,公比为2,从而求出数列{an}的通项公式;
(3)假设存在正实数m,对任意n∈N*,使bn•bn+1>0恒成立,然后根据放缩法可得 ,取n>1+b12,即n>m2+1时,有bn<0与bn>0矛盾,从而得到结论.
,取n>1+b12,即n>m2+1时,有bn<0与bn>0矛盾,从而得到结论.
解答:解(1) ;
;
∵是奇函数;
∴ 即
即
又可知和不能同时为0
故b=0
a+b+1=3c+3d,
∴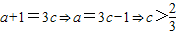
∴
当x>0时,f(x)有最大值
∴ 得
得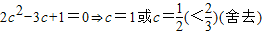
∴
(2)∵g(x)=2x2+1
∴an+12=2an2+1⇒an+12+1=2(an2+1)
∴{an2+1}为等比数列,其首项为a12+1=2,公比为2
∴an2+1=(a12+1)•2n-1=2n∴
(3)由题
∴
假设存在正实数m,对任意n∈N*,使bn•bn+1>0恒成立.
∵b1=m>0
∴bn>0恒成立.
∴
∴
又
∴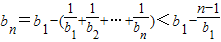
取n>1+b12,即n>m2+1时,有bn<0与bn>0矛盾.
因此,不存在正实数m,使bn•bn+1>0对n∈N*恒成立.
点评:本题主要考查了函数的解析式,以及函数的奇偶性和恒成立问题,同时考查了数列的综合运用,属于中档题.
 ,可求出c的值,从而求出函数的解析式;
,可求出c的值,从而求出函数的解析式;(2)根据an+12=g(an)可证得{an2+1}为等比数列,其首项为a12+1=2,公比为2,从而求出数列{an}的通项公式;
(3)假设存在正实数m,对任意n∈N*,使bn•bn+1>0恒成立,然后根据放缩法可得
 ,取n>1+b12,即n>m2+1时,有bn<0与bn>0矛盾,从而得到结论.
,取n>1+b12,即n>m2+1时,有bn<0与bn>0矛盾,从而得到结论.解答:解(1)
 ;
;∵是奇函数;
∴
 即
即
又可知和不能同时为0
故b=0
a+b+1=3c+3d,
∴
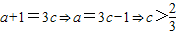
∴

当x>0时,f(x)有最大值

∴
 得
得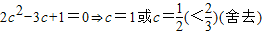
∴

(2)∵g(x)=2x2+1
∴an+12=2an2+1⇒an+12+1=2(an2+1)
∴{an2+1}为等比数列,其首项为a12+1=2,公比为2
∴an2+1=(a12+1)•2n-1=2n∴

(3)由题

∴

假设存在正实数m,对任意n∈N*,使bn•bn+1>0恒成立.
∵b1=m>0
∴bn>0恒成立.
∴

∴

又

∴
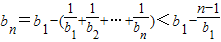
取n>1+b12,即n>m2+1时,有bn<0与bn>0矛盾.
因此,不存在正实数m,使bn•bn+1>0对n∈N*恒成立.
点评:本题主要考查了函数的解析式,以及函数的奇偶性和恒成立问题,同时考查了数列的综合运用,属于中档题.

练习册系列答案
相关题目