摘要:上一点.连结交椭圆于点.连结并延长交椭圆于点.若.求四边形的面积.解:
网址:http://m.1010jiajiao.com/timu_id_471449[举报]
 已知椭圆
已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求椭圆的标准方程;
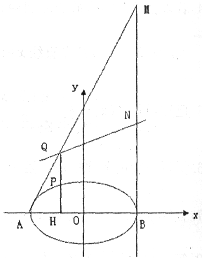
(2)过椭圆上异于A,B两点的任意一点P作PH⊥x轴,H为垂足,延长HP到点Q,且PQ=HP,过点B作直线l⊥x轴,连结AQ并延长交直线l于点M,N为MB的中点,试判断直线QN与以AB为直径的圆O的位置关系.
 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
(I)求椭圆的标准方程;
(II)设G是椭圆上异于A、B的任意一点,GH丄x轴,H为垂足,延长HG到点Q 使得HG=GQ,连接AQ并延长交直线l于点M,点N为MB的中点,判定直线QN与以AB为直径的圆O的位置关系,并证明你的结论.
已知椭圆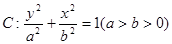 的两焦点与短轴的一个端点连结成等腰直角三角形,直线
的两焦点与短轴的一个端点连结成等腰直角三角形,直线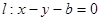 是抛物线
是抛物线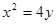 的一条切线。
的一条切线。
(1) 求椭圆方程;
(2) 直线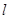 交椭圆
交椭圆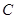 于A、B两点,若点P满足
于A、B两点,若点P满足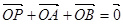 (O为坐标原点), 判断点P是否在椭圆
(O为坐标原点), 判断点P是否在椭圆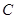 上,并说明理由。
上,并说明理由。
查看习题详情和答案>>
 的一条准线方程是
的一条准线方程是 ,其左、右顶点分别是A、B;双曲线C2:
,其左、右顶点分别是A、B;双曲线C2: 的一条渐近线方程为3x-5y=0。
的一条渐近线方程为3x-5y=0。 ,求
,求 的值。
的值。 
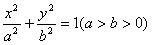 的左焦点F1(
的左焦点F1(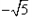 ,0),若椭圆上存在一点D,满足以椭圆短轴为直径的圆与线段DF1相切于线段DF1的中点F。
,0),若椭圆上存在一点D,满足以椭圆短轴为直径的圆与线段DF1相切于线段DF1的中点F。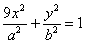 ,过点Q作斜率为k的直线l交椭圆G于H,K两点,设线段HK的中点为N,连结MN,试问当k为何值时,直线MN过椭圆G的顶点?
,过点Q作斜率为k的直线l交椭圆G于H,K两点,设线段HK的中点为N,连结MN,试问当k为何值时,直线MN过椭圆G的顶点?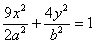 于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连结AC并延长交椭圆W于B,求证:PA⊥PB。
于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连结AC并延长交椭圆W于B,求证:PA⊥PB。