网址:http://m.1010jiajiao.com/timu_id_467631[举报]
一段长为32米的篱笆围成一个一边靠墙的矩形菜园,墙长18米,问这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
【解析】解:令矩形与墙垂直的两边为宽并设矩形宽为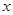 ,则长为
,则长为
所以矩形的面积 (
( ) (4分
) (4分 =128 (8分)
=128 (8分)
当且仅当 时,即
时,即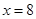 时等号成立,此时
时等号成立,此时 有最大值128
有最大值128
所以当矩形的长为 =16,宽为8时,
=16,宽为8时,
菜园面积最大,最大面积为128 (13分)答:当矩形的长为16米,宽为8米时。菜园面积最大,最大面积为128平方米(注:也可用二次函数模型解答)
查看习题详情和答案>>
改革开放以来,我国高等教育事业有了突飞猛进的发展,有人记录了某村 到
到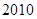 年十年间每年考入大学的人数.为方便计算,
年十年间每年考入大学的人数.为方便计算, 年编号为
年编号为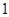 ,
,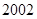 年编号为
年编号为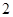 ,…,
,…,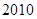 年编号为
年编号为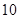 .数据如下:
.数据如下:
|
年份( |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
人数( |
3 |
5 |
8 |
11 |
13 |
14 |
17 |
22 |
30 |
31 |
(1)从这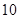 年中随机抽取两年,求考入大学的人数至少有
年中随机抽取两年,求考入大学的人数至少有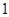 年多于
年多于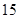 人的概率;
人的概率;
(2)根据前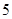 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出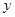 关于
关于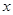 的回归方程
的回归方程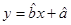 ,并计算第
,并计算第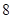 年的估计值和实际值之间的差的绝对值。
年的估计值和实际值之间的差的绝对值。
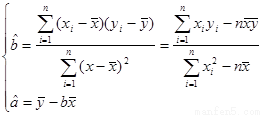
【解析】(1)设考入大学人数至少有1年多于15人的事件为A则P(A)=1-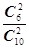 =
=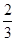 (4’)
(4’)
(2)由已知数据得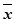 =3,
=3,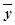 =8,
=8,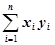 =3+10+24+44+65=146
=3+10+24+44+65=146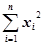 =1+4+9+16+25=55(7’)
=1+4+9+16+25=55(7’)
则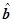 =
=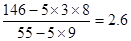 ,
,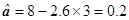 (9’)
(9’)
则回归直线方程为y=2.6x+0.2 (10’)
则第8年的估计值和真实值之间的差的绝对值为
查看习题详情和答案>>
在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等。
(1)求取出的两个球上标号为相邻整数的概率;
(2)求取出的两个球上标号之和能被3整除的概率.
【解析】本试题主要考查了古典概型概率的求解。第一问中,基本事件数为共有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)
总数为16种.其中取出的两个小球上标号为相邻整数的基本事件有:
(1,2),(2,1),(2,3),(3,2),(3,4),(4,3)共6种利用古典概型可知,P=3 /8 ;
(2)其中取出的两个小球上标号之和能被3整除的基本事件有:
(1,2),(2,1),(2,4),(3,3),(4,2)共5种可得概率值5 /16 ;
解:甲、乙两个盒子里各取出1个小球计为(X,Y)则基本事件
共有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)
总数为16种.
(1)其中取出的两个小球上标号为相邻整数的基本事件有:
(1,2),(2,1),(2,3),(3,2),(3,4),(4,3)共6种
故取出的两个小球上标号为相邻整数的概率P=3 /8 ;
(2)其中取出的两个小球上标号之和能被3整除的基本事件有:
(1,2),(2,1),(2,4),(3,3),(4,2)共5种
故取出的两个小球上标号之和能被3整除的概率为5 /16 ;
查看习题详情和答案>>
正方形ABCD的边长为1,点E在边AB上,点F在边BC上,AE=BF=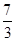 .动点P从E出发沿直线喜爱那个F运动,每当碰到正方形的方向的边时反弹,反弹时反射等于入射角,当点P第一次碰到E时,P与正方形的边碰撞的次数为
.动点P从E出发沿直线喜爱那个F运动,每当碰到正方形的方向的边时反弹,反弹时反射等于入射角,当点P第一次碰到E时,P与正方形的边碰撞的次数为
(A)16(B)14(C)12(D)10
【解析】结合已知中的点E,F的位置,进行作图,推理可知,在反射的过程中,直线是平行的,那么利用平行关系,作图,可以得到回到EA点时,需要碰撞14次即可.
查看习题详情和答案>>
某化工厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池,池的深度一定(平面图如图所示).如果池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80元/米2,水池所有墙的厚度忽略不计,试设计污水处理池的长和宽,使总造价最低,并求出最低总造价。

【解析】本试题主要考查导数在研究函数中的运用。首先设变量
设宽为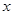 则长为
则长为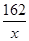 ,依题意,总造价
,依题意,总造价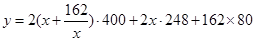
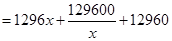
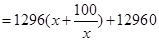
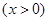
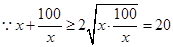 当且仅当
当且仅当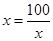 即
即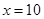 取等号
取等号
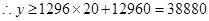 (元)得到结论。
(元)得到结论。
设宽为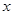 则长为
则长为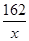 ,依题意,总造价
,依题意,总造价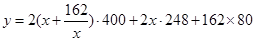
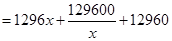
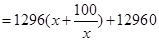
 ………6分
………6分
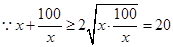 当且仅当
当且仅当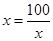 即
即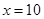 取等号
取等号
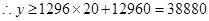 (元)……………………10分
(元)……………………10分
故当处理池宽为10米,长为16.2米时能使总造价最低,且最低总造价为38880元
查看习题详情和答案>>