摘要: , 12. , 13.或或, 14., 15..
网址:http://m.1010jiajiao.com/timu_id_467630[举报]
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:每一组[12,14);第二组[14,15)……第五组[17,18].下图是按上述分组方法得到的频率分布直方图.
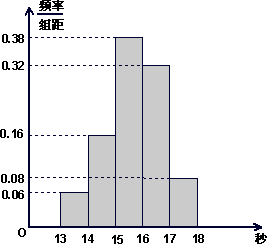
(Ⅰ)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(Ⅱ)设m、n表示该班某两位同学的百米测试成绩,且已知m,n∈[13,14)∪[17,18].
求事件“|m-n|>1”的概率.
(2012•长春模拟)某学校为了研究学情,从高三年级中抽取了20名学生三次测试的数学成绩和物理成绩,计算出了他们三次成绩的平均名次如下表:
学校规定平均名次小于或等于40.0者为优秀,大于40.0者为不优秀.
(1)对名次优秀者赋分2,对名次不优秀者赋分1,从这20名学生中随机抽取2名,用ξ表示这两名学生数学科得分的和,求ξ的分布列和数学期望;
(2)根据这次抽查数据,是否在犯错误的概率不超过0.025的前提下认为物理成绩优秀与否和数学成绩优秀与否有关系?(下面的临界值表和公式可供参考:
K2=
,其中n=a+b+c+d)
查看习题详情和答案>>
| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 数 学 | 1.3 | 12.3 | 25.7 | 36.7 | 50.3 | 67.7 | 49.0 | 52.0 | 40.0 | 34.3 |
| 物 理 | 2.3 | 9.7 | 31.0 | 22.3 | 40.0 | 58.0 | 39.0 | 60.7 | 63.3 | 42.7 |
| 学生序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数 学 | 78.3 | 50.0 | 65.7 | 66.3 | 68.0 | 95.0 | 90.7 | 87.7 | 103.7 | 86.7 |
| 物 理 | 49.7 | 46.7 | 83.3 | 59.7 | 50.0 | 101.3 | 76.7 | 86.0 | 99.7 | 99.0 |
(1)对名次优秀者赋分2,对名次不优秀者赋分1,从这20名学生中随机抽取2名,用ξ表示这两名学生数学科得分的和,求ξ的分布列和数学期望;
(2)根据这次抽查数据,是否在犯错误的概率不超过0.025的前提下认为物理成绩优秀与否和数学成绩优秀与否有关系?(下面的临界值表和公式可供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
乘某种出租车,行程不足4千米时,车票10.40元,行程不足16千米时,大于或等于4千米的部分,每0.5千米车票0.8元,计程器每0.5千米计一次价.例如当行驶路程x(千米)满足12≤x≤12.5时,按12.5千米计价;当12.5≤x<13时,按13千米计价.若某人乘车从A到B共付费28元,则从A地到B地行驶的路程m千米满足
[ ]
A.
10.5≤m<11
B.
11≤m<11.5
C.
14.5≤m<15
D.
15≤m<15.5
(2011•临沂二模)下面四个命题:
①函数y=
在(2,
)处的切线与直线2x-y+1=0垂直;
②已知a=∫
(sint+cost)dt,则(x-
)6展开式中的常数项为-
,
③在边长为1的正方形ABCD内(包括边界)有一点M,则△AMB的面积大于或等于
的概率为
④在一个2×2列联表中,由计算得K2=13,079,则其两个变量有关系的可能性是99.9%.
其中所有正确的命题序号是
查看习题详情和答案>>
①函数y=
| 1 |
| x |
| 1 |
| 2 |
②已知a=∫
|
| 1 |
| ax |
| 5 |
| 2 |
③在边长为1的正方形ABCD内(包括边界)有一点M,则△AMB的面积大于或等于
| 1 |
| 4 |
| 3 |
| 4 |
④在一个2×2列联表中,由计算得K2=13,079,则其两个变量有关系的可能性是99.9%.
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
②④
②④
.