摘要：∴S△APC= ∴四边形QAPC的面积SQAPC= S△AQC +S△APC=36-6t+6t=36(cm2) 经计算发现:点P.Q在运动的过程中.四边形QAPC的面积保持不变. (3)根据题意.应分两种情况来研究:
网址：http://m.1010jiajiao.com/timu_id_450649[举报]
如图所示，在矩形ABCD中，AB=12厘米，BC=6厘米．点P沿AB边从点A开始向点B以2厘米/秒的速度移动，点Q沿DA边从点D开始向点A以1厘米/秒的速移动，如果P、Q同时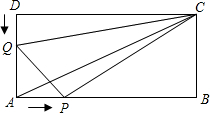
出发，用t（秒）表示移动的时间（0≤t≤6），那么：
（1）当t为何值时，△QAP为等腰直角三角形？
（2）求四边形QAPC的面积，并提出一个与计算结果有关的结论． 查看习题详情和答案>>
出发，用t（秒）表示移动的时间（0≤t≤6），那么：（1）当t为何值时，△QAP为等腰直角三角形？
（2）求四边形QAPC的面积，并提出一个与计算结果有关的结论． 查看习题详情和答案>>
如图，在直角梯形ABCD中．AB∥CD，AB=12cm，CD=6cm，DA=3cm，∠D=∠A=90°，点P沿AB边从点A开始向点B以2cm/s的速度移动；点Q沿DA边从点D开始向点A以1cm/s的速度移动，如果P、Q同时出发，用t表示移动的时间（单位：秒），并且0≤t≤3．
（1）证明不论t取何值，四边形QAPC的面积是一个定值，并且求出这个定值；
（2）请问是否存在这样的t，使得∠PCQ=90°？若存在，求出t的值；若不存在，请说明理由；
（3）请你探究△PBC能否构成直角三角形？若能，求出t的值；若不能，请说明理由．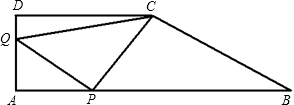
查看习题详情和答案>>
（1）证明不论t取何值，四边形QAPC的面积是一个定值，并且求出这个定值；
（2）请问是否存在这样的t，使得∠PCQ=90°？若存在，求出t的值；若不存在，请说明理由；
（3）请你探究△PBC能否构成直角三角形？若能，求出t的值；若不能，请说明理由．
查看习题详情和答案>>
如图，在长方形ABCD中，AB：BC=2：1，AB=12cm，点P沿AB边从点A开始，向点B以2cm/秒的速度移动，点Q沿DA边从点D开始向点A以1cm/秒的速度移动，如果P、Q同时出发，用t秒表示移动时间（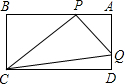
0＜t＜6）．在这运动过程中，下列结论：
①图中共有11条线段； ②图中共有19个小于平角的角；
③当t=2秒时，PB：BC=4：3 ④四边形QAPC的面积为36cm2；
其中正确的结论个数有（ ）
0＜t＜6）．在这运动过程中，下列结论：①图中共有11条线段； ②图中共有19个小于平角的角；
③当t=2秒时，PB：BC=4：3 ④四边形QAPC的面积为36cm2；
其中正确的结论个数有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
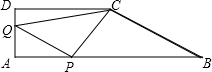速度移动，如果P、Q同时出发，用t表示移动的时间（单位：秒），并且0≤t≤3．
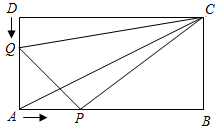如下图，在矩形ABCD中，AB=12cm，BC=6cm．点P沿AB边从点A开始向点B以2cm/s的速度移动；点Q沿DA边从点D开始向点A以1 cm/s的速度移动．如果P、Q同时出发，用t（s）表示移动的时间（0≤t≤6）那么：