网址:http://m.1010jiajiao.com/timu_id_44854[举报]
说明:
一、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解答与本解答不同,可根据试题的主要内容比照评分标准制定相应的评分细则.
二、对计算题,当考生的解答 某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分.
三、解答右端所注分数,表示考生正确做到这一步应得的累加分数.
四、只给整数分数,选择题和填空题不给中间分.
一、选择题:本题主要考查基础知识和基本运算.
1、A 2、A 3、C 4、C 5、A 6、C
7、B 8、C 9、A 10、D 11、B 12、B
二、填空题:本大题共4个小题;每小题4分,共16分.本题主要考查基础知识和基本运算.
13、2 14、0 15、2.files/image191.gif) 16、② ④
16、② ④
三、解答题:本大题共6小题,共74分,解答题应写出文字说明,证明过程或演算步骤,在答题卡上相应题目的答题区域内作答.
17.本小题主要考查三角函数的符号,诱导公式,两角和差公式,二倍角公式,三角函数的图象及单调性等基本知识以及推理和运算能力.满分12分
解:(1)∵.files/image107.gif) 且sin2
且sin2.files/image048.gif) =
=.files/image110.gif) ∴2sin
∴2sin.files/image048.gif) cos
cos.files/image048.gif) =
=.files/image110.gif) ,sin
,sin.files/image048.gif) ≥0得cos
≥0得cos.files/image048.gif) >0
>0
从而sin.files/image048.gif) +cos
+cos.files/image048.gif) >0 ………………………………………………………… 3分
>0 ………………………………………………………… 3分
∴
.files/image195.gif) =sin
=sin.files/image048.gif) +cos
+cos.files/image048.gif) =
=.files/image105.gif)
.files/image197.gif) =
=.files/image199.gif) =
=.files/image201.gif) …………6分
…………6分
(2)∵.files/image113.gif) ∴
∴.files/image101.gif) =-sinx+cosx=
=-sinx+cosx=.files/image204.gif) sin(x+
sin(x+.files/image206.gif) ) ………………………… 8分
) ………………………… 8分
∴.files/image113.gif) 时,
时,.files/image101.gif) 的单调递增区间为[
的单调递增区间为[.files/image208.gif) ,
,.files/image210.gif) ],………………………………10分
],………………………………10分
.files/image101.gif) 单调递减区间为[
单调递减区间为[.files/image210.gif) ,2
,2.files/image208.gif) ].………………………………………… 12分
].………………………………………… 12分
18.本小题主要考查等差、比数列的概念,应用通项公式及求和公式进行计算的能力.
满分12分
解:(1) .files/image213.gif) ∴
∴.files/image215.gif) ,
,
所以, 数列.files/image115.gif) 是以
是以.files/image217.gif) 为首项,
为首项,.files/image219.gif) 为公差的等差数列,………4分
为公差的等差数列,………4分
∴.files/image221.gif)
(2)由(1)得.files/image223.gif)
.files/image225.gif)
解法二:(1)同解法一
(2) 由(1)得.files/image223.gif)
∴.files/image228.gif) ……………8分,
……………8分,
∴.files/image230.gif) ,
,
∴.files/image232.gif) ,
,.files/image234.gif) ……………10分
……………10分
=.files/image236.gif)
=.files/image238.gif) ,……………………………11分
,……………………………11分
又.files/image240.gif) . ………………………12分
. ………………………12分
19.本小题主要考查直线和平面的位置关系,二面角的大小,点到平面的距离。考查空间想象能力、逻辑推理能力和运算能力.满分12分
解法一:(1)在直角梯形ABCD中,过点A做AN垂直BC,
.files/image241.gif) 垂足为N,易得BN=1,
垂足为N,易得BN=1,.files/image243.gif) 同时四边形ANCD是矩形,
同时四边形ANCD是矩形,
则CN=1,点N为BC的中点,所以点N与点M重合,.files/image245.gif) .
.
…………………………………………………………2分
连结AM,
因为.files/image247.gif) 平面ABCD,所以
平面ABCD,所以.files/image249.gif) ,又AD∥BC,
,又AD∥BC,
所以SM.files/image132.gif) AD。………4分
AD。………4分
(2)过点A做AG垂直SM,G为垂足,
易证平面SAM.files/image251.gif) ,
,
则.files/image253.gif) ,在RT
,在RT.files/image255.gif) 中,
中, .files/image257.gif) 。………7分
。………7分
又AD∥平面SBC,所以点D到平面SBC的距离为点A到平面SBC的距离AG,
点D到平面SBC的距离为.files/image259.gif) ………8分
………8分
(3)取AB中点E,因为.files/image261.gif) 是等边三角形,所以
是等边三角形,所以.files/image263.gif) ,又
,又.files/image265.gif) ,得
,得.files/image267.gif) ,过点E作EF垂直SB, F为垂足,连结CF,则
,过点E作EF垂直SB, F为垂足,连结CF,则.files/image269.gif) ,所以
,所以.files/image271.gif) 是二面角A-SB-C的平面角.………10分
是二面角A-SB-C的平面角.………10分
在RT.files/image273.gif) 中,
中,.files/image275.gif) .在RT
.在RT.files/image277.gif) 中,
中,.files/image279.gif) ,所以二面角A-SB-C的大小为
,所以二面角A-SB-C的大小为.files/image281.gif) .………12分
.………12分
解法二:(1)同解法一.
(2)根据(1),如图所示,分别以AM,AD,AC所在射线为x,y,z轴建立空间直角坐标系.
有A(0,0,0),M(.files/image283.gif) ,0,0),B(
,0,0),B(.files/image283.gif) ,-1,0),C(
,-1,0),C(.files/image283.gif) ,1 ,0),D(0,1 ,0),S(0,0 ,1)
,1 ,0),D(0,1 ,0),S(0,0 ,1)
所以.files/image287.gif) ,
,.files/image289.gif) ,
,.files/image291.gif) .
.
设平面SBC的法向量.files/image293.gif) ,则
,则.files/image295.gif) ,
,
即 .files/image297.gif) ,
,
解得.files/image299.gif) ,取
,取.files/image301.gif) .………6分
.………6分
又.files/image303.gif) =
=.files/image305.gif) ,则点D到平面SBC的距离
,则点D到平面SBC的距离
.files/image307.gif) .………8分
.………8分
(3)设平面ASB的法向量.files/image309.gif) ,则
,则.files/image311.gif) ,
,
即.files/image313.gif) ,
,
解得.files/image315.gif) ,取
,取.files/image317.gif) .………10分
.………10分
∴.files/image319.gif) ,则二面角A-SB-C的大小为
,则二面角A-SB-C的大小为.files/image321.gif) .………12分
.………12分
20.本小题主要考查排列组合与概率的基础知识,考查推理、运算能力与分类讨论思想,以及运用数学知识解决实际问题的能力. 满分12分
解:(1)因为掷出1点的概率为.files/image323.gif) ,
,
所以甲盒中有3个球的概率.files/image325.gif) ………………………4分
………………………4分
(2)甲、乙、丙3个盒中的球数依次成等差数列有以下三种情况:
.files/image105.gif) ①甲、乙、丙3个盒中的球数分别为0、1、2,
①甲、乙、丙3个盒中的球数分别为0、1、2,
此时的概率.files/image327.gif) ……………………………6分
……………………………6分
②甲、乙、丙3个盒中的球数分别为1、1、1,
此时的概率.files/image329.gif) ……………………………8分
……………………………8分
③甲、乙、丙3个盒中的球数分别为2、1、0,
此时的概率.files/image331.gif) ……………………………10分
……………………………10分
所以,甲、乙、丙3个盒中的球数依次成等差数列的概率.files/image333.gif) …12分
…12分
21.本小题主要考查函数的单调性、最值等基本知识;考查函数与方程、数形结合、分类与整合等数学思想方法;考查运用数学知识分析和解决实际问题的能力以及运算能力,满分12分.
解(Ⅰ).files/image335.gif)
.files/image337.gif) 上单调递增,在[-2,2]上单调递减,
上单调递增,在[-2,2]上单调递减,
.files/image339.gif) ,……2分
,……2分
.files/image341.gif) ,
,
.files/image343.gif) …………………………4分
…………………………4分
又.files/image345.gif)
.files/image347.gif)
.files/image349.gif) ……………………………………………………6分
……………………………………………………6分
(Ⅱ)已知条件等价于在.files/image351.gif) ……………………8分
……………………8分
.files/image353.gif) 上为减函数,
上为减函数,
且.files/image355.gif) ……………………………………10分
……………………………………10分
.files/image357.gif) 上为减函数,
上为减函数,
.files/image359.gif)
又.files/image361.gif) ………………………………………………12分
………………………………………………12分
22.本小题主要考查直线、椭圆、向量等基础知识,以及应用这些知识研究曲线几何特征
基本方法,考查运算能力和综合解题能力.满分14分.
解:(1)当.files/image173.gif) 时
时.files/image189.gif) ,
,.files/image363.gif) ,
,
消去.files/image365.gif) 得:
得: .files/image367.gif) , ………2分
, ………2分
此时ㄓ>0,
设.files/image369.gif) 点坐标为
点坐标为 .files/image371.gif) ,
, .files/image373.gif) 点坐标为
点坐标为.files/image375.gif) ,
,
则有.files/image377.gif) =
=.files/image379.gif) , 3
, 3
.files/image381.gif) =
=.files/image383.gif) , 4
, 4
.files/image385.gif)
.files/image175.gif) ,∴
,∴ .files/image387.gif) ,代入3、4得
,代入3、4得
.files/image389.gif) 消去
消去.files/image391.gif) 得
得.files/image393.gif)
解得,.files/image395.gif)
则所求椭圆C的方程.files/image397.gif) .……………………6分
.……………………6分
(2) 当.files/image177.gif) 2时,椭圆C的方程
2时,椭圆C的方程.files/image399.gif) ,………………7分
,………………7分
设.files/image369.gif) 点坐标为
点坐标为 .files/image371.gif) ,
, .files/image373.gif) 点坐标为
点坐标为.files/image375.gif) ,
,
直线.files/image179.gif) 的方程为:
的方程为:.files/image402.gif) ,
,
与.files/image167.gif) 的方程:
的方程: .files/image404.gif) 联立得: M点的纵坐标
联立得: M点的纵坐标.files/image406.gif) ,
,
同理可得: .files/image408.gif) ,………………9分
,………………9分
则.files/image188.gif) =
=.files/image411.gif)
.files/image413.gif)
.files/image415.gif)
.files/image417.gif)
.files/image419.gif) …10分
…10分
.files/image385.gif)
.files/image422.gif)
.files/image424.gif) ,
,
此时ㄓ>0,由 .files/image377.gif) =
=.files/image426.gif) ,
,.files/image381.gif) =
=.files/image428.gif) ,
,
.files/image430.gif) =
=.files/image432.gif) ,
,.files/image434.gif) =
=.files/image436.gif) ,……………… 12分
,……………… 12分
则.files/image188.gif)
.files/image438.gif)
.files/image440.gif)
.files/image442.gif) ,
,
.files/image444.gif) ……………………13分
……………………13分
.files/image446.gif) (当
(当.files/image448.gif) 时取等号),
时取等号),
∴.files/image188.gif) 的最小值为6. ……………………14分
的最小值为6. ……………………14分
给出下列四个命题:
①异面直线是指空间既不平行又不相交的直线;
②两异面直线 ,如果
,如果 平行于平面
平行于平面 ,那么
,那么 不平行平面
不平行平面 ;
;
③两异面直线 ,如果
,如果 平面
平面 ,那么
,那么 不垂直于平面
不垂直于平面 ;
;
④两异面直线在同一平面内的射影不可能是两条平行直线 。
其中正确的命题是_________________。
查看习题详情和答案>>
①异面直线是指空间既不平行又不相交的直线;
②两异面直线
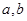 ,如果
,如果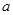 平行于平面
平行于平面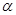 ,那么
,那么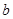 不平行平面
不平行平面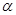 ;
;③两异面直线
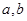 ,如果
,如果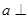 平面
平面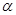 ,那么
,那么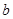 不垂直于平面
不垂直于平面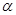 ;
;④两异面直线在同一平面内的射影不可能是两条平行直线 。
其中正确的命题是_________________。
给出下列四个命题:①异面直线是指空间既不平行又不相交的直线;②两异面直线a,b,如果a平行于平面α,那么b不平行平面α;③两异面直线a,b,如果a⊥平面α,那么b不垂直于平面α;④两异面直线在同一平面内的射影不可能是两条平行直线.其中正确的命题是________
 .
.