摘要:∴当时.命题成立.
网址:http://m.1010jiajiao.com/timu_id_447818[举报]
下列命题成立的是
①a,bc∈R,a2+b2+c2≥ab+bc+ac;
②当x>0时,函数f(x)=
+2x≥2
=2
,∴当且仅当x2=2x即x=2时f(x)取最小值;
③当x>1时,
≥5;
④当x>0时,x+
+
的最小值为
.
查看习题详情和答案>>
①③④
①③④
. (写出所有正确命题的序号).①a,bc∈R,a2+b2+c2≥ab+bc+ac;
②当x>0时,函数f(x)=
| 1 |
| x2 |
|
|
③当x>1时,
| x2-x+4 |
| x-1 |
④当x>0时,x+
| 1 |
| x |
| 1 | ||
x+
|
| 5 |
| 2 |
当a,b是非零实数时,以下四个命题都成立:
①a+
≠0; ②(a+b)2=a2+2ab+b2;
③若|a|=|b|,则a=±b; ④若a2=ab,则a=b.
那么,当a,b是非零复数时,仍然保证成立的命题是( )
①a+
| 1 |
| a |
③若|a|=|b|,则a=±b; ④若a2=ab,则a=b.
那么,当a,b是非零复数时,仍然保证成立的命题是( )
| A、①② | B、②③ | C、③④ | D、②④ |
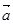 ∥
∥ ,
,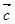 ,则
,则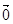 时成立 C.当
时成立 C.当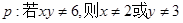 ,命题
,命题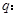 当
当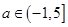 时,
时,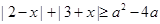 对任意
对任意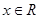 恒成立,则 (
)
恒成立,则 (
)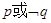 ”为假命题 B.“
”为假命题 B.“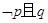 ”
为真命题
”
为真命题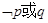 “为假命题 D.“
“为假命题 D.“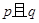 ”为真命题
”为真命题