摘要:即对一切有:, 从而判别式??????????????????????????????12分
网址:http://m.1010jiajiao.com/timu_id_447804[举报]
已知数列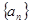 满足
满足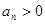 且对一切
且对一切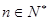 ,
,
有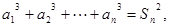
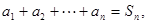
(Ⅰ)求证:对一切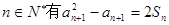
(Ⅱ)求数列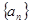 通项公式.
通项公式.
(Ⅲ)求证: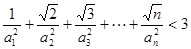
【解析】第一问利用,已知表达式,可以得到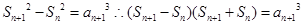 ,然后得到
,然后得到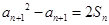 ,从而求证
。
,从而求证
。
第二问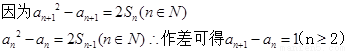 ,可得数列的通项公式。
,可得数列的通项公式。
第三问中,利用放缩法的思想,我们可以得到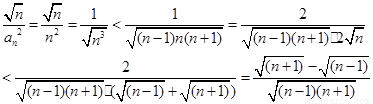
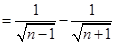 然后利用累加法思想求证得到证明。
然后利用累加法思想求证得到证明。
解: (1) 证明:
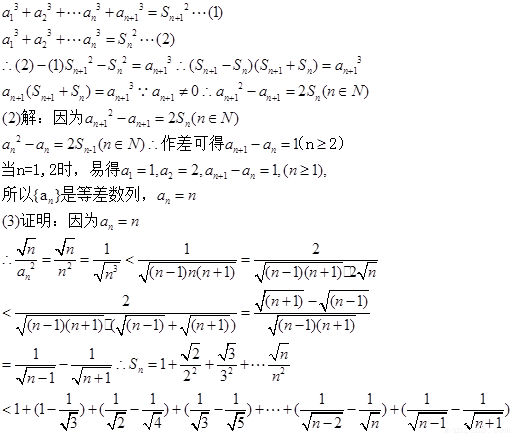
查看习题详情和答案>>
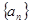 的前
的前 项和为
项和为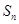 ,
,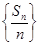 为等差数列,证明
为等差数列,证明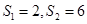 ,求数列
,求数列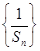 的前
的前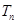 ;
;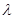 使得对一切
使得对一切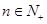 ,有
,有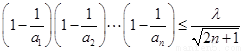 成立,求
成立,求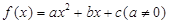 满足
满足 ,
,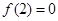 ,且方程
,且方程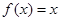 有等根.(1)求
有等根.(1)求 的解析式;
的解析式;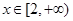 有不等式
有不等式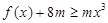 成立,求实数
成立,求实数 的取值范围.
的取值范围.