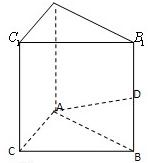
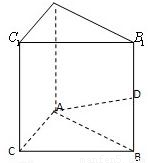
摘要:ABCD是四边形.点P 是平面ABCD外一点.M是PC的中点.在DM上取一点G.过G和AP作平面交平面BDM于GH.求证:AP||GH.
网址:http://m.1010jiajiao.com/timu_id_4468281[举报]
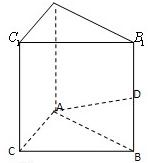 P是平面ABCD外的点,四边形ABCD是平行四边形,
P是平面ABCD外的点,四边形ABCD是平行四边形,| AB |
| AD |
| AP |
(1)求证:PA⊥平面ABCD;
(2)对于向量
| a |
| b |
| c |
| a |
| b |
| c |
| AB |
| AD |
| AP |
| AB |
| AD |
| AP |
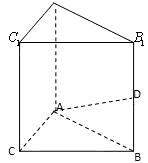 P是平面ABCD外的点,四边形ABCD是平行四边形,
P是平面ABCD外的点,四边形ABCD是平行四边形, =(2,-1,-4),
=(2,-1,-4), =(4,2,0),
=(4,2,0), =(-1,2,-1).
=(-1,2,-1).
(1)求证:PA⊥平面ABCD;
(2)对于向量 =(x1,y1z1),
=(x1,y1z1),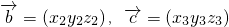 ,定义一种运算:
,定义一种运算: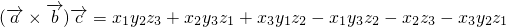 ,试计算
,试计算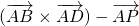 的绝对值;说明其与几何体P-ABCD的体积关系,并由此猜想向量这种运算
的绝对值;说明其与几何体P-ABCD的体积关系,并由此猜想向量这种运算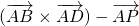 的绝对值的几何意义.
的绝对值的几何意义.
查看习题详情和答案>>
P是平面ABCD外的点,四边形ABCD是平行四边形,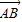 =(2,-1,-4),
=(2,-1,-4),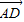 =(4,2,0),
=(4,2,0),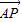 =(-1,2,-1).
=(-1,2,-1).
(1)求证:PA⊥平面ABCD;
(2)对于向量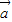 =(x1,y1z1),
=(x1,y1z1),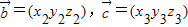 ,定义一种运算:
,定义一种运算: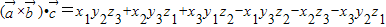 ,试计算
,试计算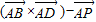 的绝对值;说明其与几何体P-ABCD的体积关系,并由此猜想向量这种运算
的绝对值;说明其与几何体P-ABCD的体积关系,并由此猜想向量这种运算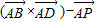 的绝对值的几何意义.
的绝对值的几何意义.
 查看习题详情和答案>>
查看习题详情和答案>>
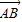 =(2,-1,-4),
=(2,-1,-4),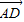 =(4,2,0),
=(4,2,0),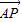 =(-1,2,-1).
=(-1,2,-1).(1)求证:PA⊥平面ABCD;
(2)对于向量
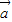 =(x1,y1z1),
=(x1,y1z1),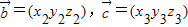 ,定义一种运算:
,定义一种运算: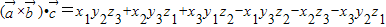 ,试计算
,试计算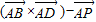 的绝对值;说明其与几何体P-ABCD的体积关系,并由此猜想向量这种运算
的绝对值;说明其与几何体P-ABCD的体积关系,并由此猜想向量这种运算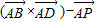 的绝对值的几何意义.
的绝对值的几何意义. 查看习题详情和答案>>
查看习题详情和答案>>
 =(2,-1,-4),
=(2,-1,-4), =(4,2,0),
=(4,2,0), =(-1,2,-1).
=(-1,2,-1). =(x1,y1z1),
=(x1,y1z1), ,定义一种运算:
,定义一种运算: ,试计算
,试计算 的绝对值;说明其与几何体P-ABCD的体积关系,并由此猜想向量这种运算
的绝对值;说明其与几何体P-ABCD的体积关系,并由此猜想向量这种运算 的绝对值的几何意义.
的绝对值的几何意义.