题目内容
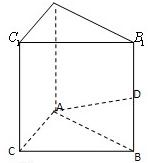P是平面ABCD外的点，四边形ABCD是平行四边形，| AB |
| AD |
| AP |
（1）求证：PA⊥平面ABCD；
（2）对于向量
| a |
| b |
| c |
| a |
| b |
| c |
| AB |
| AD |
| AP |
| AB |
| AD |
| AP |
分析：（1）证明
与平面ABCD内的两个不共线的向量垂直，即证明
与此平面内的两个不共线的向量的数量积等于0．
（2）根据体题中定义的运算法则，化简 |(
×
)•
| 的结果，发现此值正好等于以AB，AD，AP为棱的平行六面体的体积．
| AP |
| AP |
（2）根据体题中定义的运算法则，化简 |(
| AB |
| AD |
| AP |
解答：解：（1）
•
=(2，-1，-4)•(-1，2，-1)=-2+(-2)+4=0，∴
⊥
，即AP⊥AB．
•
=(-1，2，-1)•(4，2，0)=-4+4+0=0，即PA⊥AD．
∴PA⊥面ABCD．
（2）|(
×
)•
|=48，又cos?
•
＞=
，
V=
|
|•|
|•sin?
•
＞•|
|=16
猜测：|(
×
)•
|在几何上可表示以AB，AD，AP为棱的平行六面体的体积（或以AB，AD，AP为棱的四棱柱的体积）．
| AP |
| AB |
| AP |
| AB |
| AP |
| AD |
∴PA⊥面ABCD．
（2）|(
| AB |
| AD |
| AP |
| AB |
| AD |
| 3 | ||
|
V=
| 1 |
| 3 |
| AB |
| AD |
| AB |
| AD |
| AP |
猜测：|(
| AB |
| AD |
| AP |
点评：本题考查直线和平面垂直的方法，以及利用题中的新定义的运算法则计算|(
×
)•
|的结果，体现了数形结合的数学思想，属于中档题．
| AB |
| AD |
| AP |
练习册系列答案
相关题目
9、如图，已知四边形ABCD是平行四边形，点P是平面ABCD外的一点，则在四棱锥P-ABCD中，M是PC的中点，在DM上取一点G，过G和AP作平面交平面BDM于GH．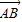
=（2，-1，-4），
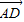=（4，2，0），
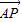=（-1，2，-1）．
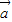=（x1，y1z1），
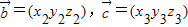，定义一种运算：
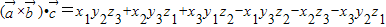，试计算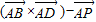
的绝对值；说明其与几何体P-ABCD的体积关系，并由此猜想向量这种运算
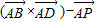的绝对值的几何意义．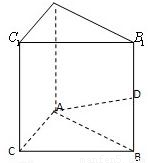
=（2，-1，-4），
=（4，2，0），
=（-1，2，-1）．
=（x1，y1z1），
，定义一种运算：
，试计算
的绝对值；说明其与几何体P-ABCD的体积关系，并由此猜想向量这种运算
的绝对值的几何意义．
如图，已知四边形ABCD是平行四边形，点P是平面ABCD外的一点，则在四棱锥P-ABCD中，M是PC的中点，在DM上取一点G，过G和AP作平面交平面BDM于GH．求证：AP∥GH．