摘要：求下列函数的单调递增区间: (1)y=,(2)y= 解 (1)函数的定义域为R. 令u=6+x-2x2,则y=()u. ∵二次函数u=6+x-2x2的对称轴为x=, 在区间［.+∞)上.u=6+x-2x2是减函数. 又函数y=()u是减函数. ∴函数y=在［.+∞)上是增函数. 故y=的单调递增区间为［.+∞). (2)令u=x2-x-6,则y=2u, ∵二次函数u=x2-x-6的对称轴是x=, 在区间［.+∞)上u=x2-x-6是增函数. 又函数y=2u为增函数. ∴函数在区间［.+∞)上是增函数. 故函数的单调递增区间是［.+∞).
网址：http://m.1010jiajiao.com/timu_id_4463461[举报]
对于函数y＝f(x)(x∈D，D是此函数的定义域)若同时满足下列条件：
(Ⅰ)f(x)在D内单调递增或单调递减；
(Ⅱ)存在区间[a，b]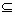
D，使f(x)在[a，b]上的值域为[a，b]；那么，把y＝f(x)(x∈D)叫闭函数．
(1)求闭函数y＝－x3符合条件(Ⅱ)的区间[a，b]；
(2)判断函数f(x)＝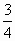
x＋
(x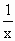∈R+)是否为闭函数？并说明理由；
(3)若y＝k＋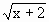
是闭函数，求实数k的取值范围．
已知y=f(x)(x∈D，D为此函数的定义域)同时满足下列两个条件：①函数f(x)在D内单调递增或单调递减；②如果存在区间[a，b]
D，使函数f(x)在区间[a，b]上的值域为[a，b]，那么称y=f(x)，x∈D为闭函数；请解答以下问题：
（1）求闭函数y=-x3符合条件②的区间；
（2）判断函数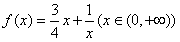
是否为闭函数？并说明理由；
（3）若y=k+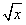
(k＜0)是闭函数，求实数k的取值范围。
查看习题详情和答案>>
D，使函数f(x)在区间[a，b]上的值域为[a，b]，那么称y=f(x)，x∈D为闭函数；请解答以下问题：（1）求闭函数y=-x3符合条件②的区间；
（2）判断函数
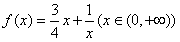是否为闭函数？并说明理由；（3）若y=k+
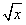(k＜0)是闭函数，求实数k的取值范围。 已知y=f（x）（x∈D，D为此函数的定义域）同时满足下列两个条件：①函数f（x）在D内单调递增或单调递减；②如果存在区间[a，b]⊆D，使函数f（x）在区间[a，b]上的值域为[a，b]，那么称y=f（x），x∈D为闭函数；请解答以下问题：
（1）求闭函数y=-x3符合条件②的区间[a，b]；
（2）判断函数f(x)=
x+
(x∈(0，+∞))是否为闭函数？并说明理由；
（3）若y=k+
(k＜0)是闭函数，求实数k的取值范围．
查看习题详情和答案>>
（1）求闭函数y=-x3符合条件②的区间[a，b]；
（2）判断函数f(x)=
| 3 |
| 4 |
| 1 |
| x |
（3）若y=k+
| x |