题目内容
已知y=f(x)(x∈D,D为此函数的定义域)同时满足下列两个条件:①函数f(x)在D内单调递增或单调递减;②如果存在区间[a,b] D,使函数f(x)在区间[a,b]上的值域为[a,b],那么称y=f(x),x∈D为闭函数;请解答以下问题:
D,使函数f(x)在区间[a,b]上的值域为[a,b],那么称y=f(x),x∈D为闭函数;请解答以下问题:
(1)求闭函数y=-x3符合条件②的区间;
(2)判断函数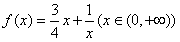 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)若y=k+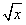 (k<0)是闭函数,求实数k的取值范围。
(k<0)是闭函数,求实数k的取值范围。
 D,使函数f(x)在区间[a,b]上的值域为[a,b],那么称y=f(x),x∈D为闭函数;请解答以下问题:
D,使函数f(x)在区间[a,b]上的值域为[a,b],那么称y=f(x),x∈D为闭函数;请解答以下问题:(1)求闭函数y=-x3符合条件②的区间;
(2)判断函数
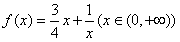 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;(3)若y=k+
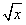 (k<0)是闭函数,求实数k的取值范围。
(k<0)是闭函数,求实数k的取值范围。 解:(1)先证y=-x3符合条件①:对于任意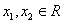 ,且
,且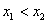 ,
,
有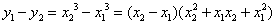
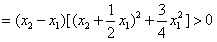 ,
,
∴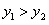 ,故y=-x3是R上的减函数,
,故y=-x3是R上的减函数,
由题意得: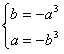 ,则
,则 ,
,
∴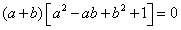 而
而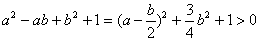 ,
,
∴a+b=0,
又b>a,
∴a=-1,b=1,即所求区间为[-1,1]。
(2)当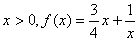 在
在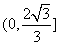 上单调递减,在
上单调递减,在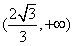 上单调递增,(证明略);
上单调递增,(证明略);
所以,函数在定义域上不是单调递增或单调递减函数,从而该函数不是闭函数。
(3)易知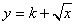 是
是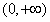 上的增函数,符合条件①;
上的增函数,符合条件①;
设函数符合条件②的区间为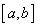 ,
,
则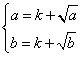 ,故a,b是
,故a,b是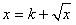 的两个不等根,
的两个不等根,
即方程组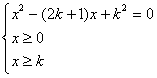 有两个不等非负实根;
有两个不等非负实根;
设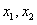 为方程的二根,则
为方程的二根,则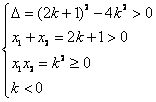 ,
,
解得: ,
,
∴k的取值范围是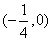 。
。
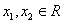 ,且
,且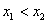 ,
,有
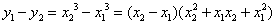
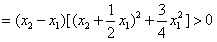 ,
,∴
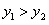 ,故y=-x3是R上的减函数,
,故y=-x3是R上的减函数,由题意得:
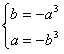 ,则
,则 ,
,∴
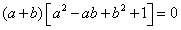 而
而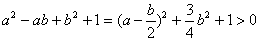 ,
,∴a+b=0,
又b>a,
∴a=-1,b=1,即所求区间为[-1,1]。
(2)当
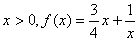 在
在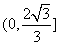 上单调递减,在
上单调递减,在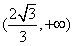 上单调递增,(证明略);
上单调递增,(证明略);所以,函数在定义域上不是单调递增或单调递减函数,从而该函数不是闭函数。
(3)易知
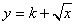 是
是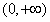 上的增函数,符合条件①;
上的增函数,符合条件①;设函数符合条件②的区间为
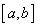 ,
,则
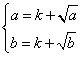 ,故a,b是
,故a,b是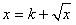 的两个不等根,
的两个不等根,即方程组
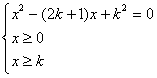 有两个不等非负实根;
有两个不等非负实根;设
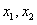 为方程的二根,则
为方程的二根,则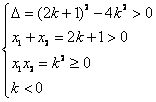 ,
,解得:
 ,
,∴k的取值范围是
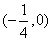 。
。 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知y=f(x)是奇函数,且满足f(x+1)=f(x-1),当x∈(0,1)时,f(x)=log2
,则y=f(x)在(1,2)内是( )
| 1 |
| 1-x |
| A、单调增函数,且f(x)<0 |
| B、单调减函数,且f(x)>0 |
| C、单调增函数,且f(x)>0 |
| D、单调减函数,且f(x)<0 |