摘要:例1 判断下列命题是否正确.若不正确.请简述理由. ①向量与是共线向量.则A.B.C.D四点必在一直线上, ②单位向量都相等, ③任一向量与它的相反向量不相等, ④四边形ABCD是平行四边形的充要条件是= ⑤模为0是一个向量方向不确定的充要条件, ⑥共线的向量.若起点不同.则终点一定不同. 解:①不正确.共线向量即平行向量.只要求方向相同或相反即可.并不要求两个向量.在同一直线上. ②不正确.单位向量模均相等且为1.但方向并不确定. ③不正确.零向量的相反向量仍是零向量.但零向量与零向量是相等的. ④.⑤正确.⑥不正确.如图与共线.虽起点不同.但其终点却相同. 评述:本题考查基本概念.对于零向量.单位向量.平行向量.共线向量的概念特征及相互关系必须把握好. 例2下列命题正确的是( ) A.a与b共线.b与c共线.则a与c也共线 B.任意两个相等的非零向量的始点与终点是一平行四边形的四顶点 C.向量a与b不共线.则a与b都是非零向量 D.有相同起点的两个非零向量不平行 解:由于零向量与任一向量都共线.所以A不正确,由于数学中研究的向量是自由向量.所以两个相等的非零向量可以在同一直线上.而此时就构不成四边形.根本不可能是一个平行四边形的四个顶点.所以B不正确,向量的平行只要方向相同或相反即可.与起点是否相同无关.所以D不正确,对于C.其条件以否定形式给出.所以可从其逆否命题来入手考虑.假若a与b不都是非零向量.即a与b至少有一个是零向量.而由零向量与任一向量都共线.可有a与b共线.不符合已知条件.所以有a与b都是非零向量.所以应选C. 评述:对于有关向量基本概念的考查.可以从概念的特征入手.也可以从反面进行考虑.要启发学生注意这两方面的结合
网址:http://m.1010jiajiao.com/timu_id_4461818[举报]
判断下列命题是否正确,若不正确,请简述理由.
①向量![]() 与
与![]() 是共线向量,则A、B、C、D四点必在一直线上;
是共线向量,则A、B、C、D四点必在一直线上;
②单位向量都相等;
③任一向量与它的相反向量不相等;
④四边形ABCD是平行四边形的充要条件是![]() =
=![]()
⑤模为0是一个向量方向不确定的充要条件;
⑥共线的向量,若起点不同,则终点一定不同.
查看习题详情和答案>>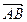 与
与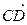 是共线向量,则A、B、C、D四点必在一直线上;
是共线向量,则A、B、C、D四点必在一直线上;
 与
与 是共线向量,则A、B、C、D四点必在同一直线上;
是共线向量,则A、B、C、D四点必在同一直线上; ;
;