（2009•闵行区二模）（理）在长方体ABCD-A₁B₁C₁D₁中，AB=2，AD=1，AA₁=1，点E在棱AB上移动．
（1）探求AE等于何值时，直线D₁E与平面AA₁D₁D成45°角；
（2）点E移动为棱AB中点时，求点E到平面A₁DC₁的距离．

（2012•江苏二模）如图，已知椭圆C：

x2

4

+y2=1，A、B是四条直线x=±2，y=±1所围成的两个顶点．
（1）设P是椭圆C上任意一点，若

OP

=m

OA

+n

OB

，求证：动点Q（m，n）在定圆上运动，并求出定圆的方程；
（2）若M、N是椭圆C上两个动点，且直线OM、ON的斜率之积等于直线OA、OB的斜率之积，试探求△OMN的面积是否为定值，说明理由．

已知定义在R上的二次函数R（x）=ax²+bx+c满足2^R（-x）-2^R（x）=0，且R（x）的最小值为0，函数h（x）=lnx，又函数f（x）=h（x）-R（x）．
（I）求f（x）的单调区间；  
（II）当a≤

1

2

时，若x₀∈[1，3]，求f（x₀）的最小值；
（III）若二次函数R（x）图象过（4，2）点，对于给定的函数f（x）图象上的点A（x₁，y₁），当x1=

3

2

时，探求函数f（x）图象上是否存在点B（x₂，y₂）（x₂＞2），使A、B连线平行于x轴，并说明理由．（参考数据：e=2.71828…）

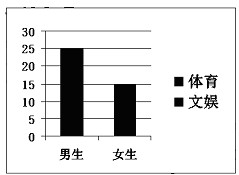对某班学生是更喜欢体育还是更喜欢文娱进行调查，根据调查得到的数据，所绘制的二维条形图如图．
（I）根据图中数据，制作2×2列联表；
（II）若要从更喜欢体育的学生中随机选3人，组成体育爱好者交流小组，去外校参观学习，求小组中含女生人数的分布列和期望．

已知定义在R上的二次函数R（x）=ax²+bx（a＞0）是偶函数，函数f（x）=2lnx-R（x）．
（I）求f（x）的单调区间；  
（II）当a≤1时，若x₀∈[1，2]，求f（x₀）的最大值；
（III）若二次函数R（x）图象过（1，1）点，对于给定的函数f（x）图象上的点A（x₁，y₁），当x₁=

1

e

时，探求函数f（x）图象上是否存在点B（x₂，y₂）（x₂＞1），使A、B连线平行于x轴，并说明理由．（参考数据：e=2.71828…）