题目内容
已知定义在R上的二次函数R(x)=ax
2+bx(a>0)是偶函数,函数f(x)=2lnx-R(x).
(I)求f(x)的单调区间;
(II)当a≤1时,若x
0∈[1,2],求f(x
0)的最大值;
(III)若二次函数R(x)图象过(1,1)点,对于给定的函数f(x)图象上的点A(x
1,y
1),当x
1=
时,探求函数f(x)图象上是否存在点B(x
2,y
2)(x
2>1),使A、B连线平行于x轴,并说明理由.(参考数据:e=2.71828…)
分析:(I)根据二次函数的图象和性质及偶函数的图象关于Y轴对称,可求出函数f(x)的解析式,进而利用导数法,可求出f(x)的单调区间;
(II)由(I)中结论中函数f(x)的单调性,可得x=
是函数f(x)的极小值点,对a分类讨论可得x
0∈[1,2],求f(x
0)的最大值;
(III)由函数R(x)图象过(1,1)点,可求出a值,确定函数f(x)的解析式,构造函数g(x)=f(x)-f(
),分析函数零点是否存在可得答案.
解答:解:(I)∵定义在R上的二次函数R(x)=ax
2+bx(a>0)是偶函数,
∴函数的对称轴x=
=0,即b=0,
∴R(x)=ax
2,
∴f(x)=2lnx-ax
2的定义域为(0,+∞)
∴f′(x)=
,
令f′(x)>0,则0<x<
令f′(x)<0,则x>
∴f(x)的单调递增区间为(0,
),单调递减区间为(
,+∞)
(II)由(1)得f(x)的单调递增区间为(0,
),单调递减区间为(
,+∞)
∴x=
是函数f(x)的极小值点
∵0<a≤1
∴
≥1
当
≥2,即0<a≤
,f(x)在区间[1,2]上递增,则f(x
0)的最大值为f(2)=2ln2-4a
当1≤
<2,即
<a≤1,则f(x
0)的最大值为f(
)=-lna-1
(III)∵二次函数R(x)图象过(1,1)点,则a=1
则f(x)=2lnx-x
2(x>0)
由(1)可知f(x)的单调递增区间为(0,1),单调递减区间为(1,+∞)
令g(x)=f(x)-f(
)=2lnx-x
2-(-2-
)
由题意可知g(x)在(1,+∞)上必存在零点
又由g(x)单调性与f(x)相同,故g(x)在(1,+∞)上单调递减
g(1)=-1-(-2-
)=1+
>0
g(e)=2-e
2-(-2-
)=4+
-e
2<0
故存在点B使A、B连线平行于x轴
点评:本题考查的知识点是函数的单调性及单调区间,二次函数在闭区间上的最值,函数的零点,是函数图象和性质的综合应用,难度较大.
 一题一题找答案解析太慢了
一题一题找答案解析太慢了
下载作业精灵直接查看整书答案解析立即下载
练习册系列答案
相关题目

 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
 满足
满足 ,且
,且 的最小值
的最小值 ,又函数
,又函数 。
。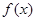 的单调区间; (II)当
的单调区间; (II)当 ≤
≤ 时,若
时,若 ,求
,求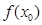 的最小值;
的最小值; ),
), 时,探求函数
时,探求函数 (
( )(
)( ),使
),使 、
、 轴,并说明理由。(参考数据:e=2.71828…)
轴,并说明理由。(参考数据:e=2.71828…) 满足
满足 ,且
,且 的最小值为0,函数
的最小值为0,函数 ,又函数
,又函数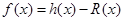 。
。 的单调区间;
的单调区间; ≤
≤ 时,若
时,若 ,求
,求 的最小值;
的最小值; ),当
),当 时,探求函数
时,探求函数 )(
)( ),使A、B连线平行于x轴,并说明理由。
),使A、B连线平行于x轴,并说明理由。