摘要: 通过具体函数.直观了解对数函数模型所刻画的数量关系.初步理解对数函数的概念.掌握f(x)=logax符号及意义.体会对数函数是一类重要的函数模型.能借助计算器或计算机画出具体对数函数的图象.探索并了解对数函数的有关性质.
网址:http://m.1010jiajiao.com/timu_id_4460186[举报]
14、在中学数学中,从特殊到一般,从具体到抽象是常见的一种思维方式.如从指数函数中可抽象出f(x1+x2)=f(x1)•f(x2)的性质;从对数函数中可抽象出f(x1•x2)=f(x1)+f(x2)的性质,那么从函数
查看习题详情和答案>>
y=kx(k≠0)
.(写出一个具体函数即可)可抽象出f(x1+x2)=f(x1)+f(x2)的性质.
函数f(x)满足:(1)定义域是(0,+∞);(2)当x>1时,f(x)<2;(3)对任意x,y∈(0,+∞),总有f(xy)=f(x)+f(y)-2.则
(1)求出f(1)的值;
(2)写出一个满足上述条件的具体函数;
(3)判断函数f(x)的单调性,并用定义加以证明. 查看习题详情和答案>>
(1)求出f(1)的值;
(2)写出一个满足上述条件的具体函数;
(3)判断函数f(x)的单调性,并用定义加以证明. 查看习题详情和答案>>
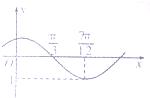 (2013•蚌埠二模)已知函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<
(2013•蚌埠二模)已知函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<