摘要:3.情态与价值 利用函数的单调性和图象求函数的最大(小)值.解决日常生活中的实际问题.激发学生学习的积极性.
网址:http://m.1010jiajiao.com/timu_id_4460149[举报]
某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B 两种产品共50件.已知生产一件A产品,需要甲种原料共9kg,乙种原料3kg,可获利润700元;生产一件B种产品,需用甲种原料4kg,乙种原料10kg,可获利润1200元.
(Ⅰ)按要求安排A,B两种产品的生产件数,有几种方案?请你设计出来.
(Ⅱ)设生产A,B两种产品获总利润y(元),其中一种的生产件数为x,试写出y与x之间的函数关系式,并利用函数性质说明(Ⅰ)中哪种方案获利最大?最大利润是多少?
查看习题详情和答案>>
(Ⅰ)按要求安排A,B两种产品的生产件数,有几种方案?请你设计出来.
(Ⅱ)设生产A,B两种产品获总利润y(元),其中一种的生产件数为x,试写出y与x之间的函数关系式,并利用函数性质说明(Ⅰ)中哪种方案获利最大?最大利润是多少?
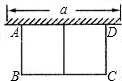 如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为Xm,面积为Sm2,
如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为Xm,面积为Sm2,(1)求S与X的函数关系式;
(2)如果要围成面积为45m2的花圃,AB的长是多少米?
(3)能围成面积比45m2更大的花圃吗?如果能,请求出最大面积.并说明围法;如果不能,请说明理由.
定义:对于任意x∈[0,1],函数f(x)≥0恒成立,且当x1≥0,x2≥0,x1+x2≤1时,总有f(x1+x2)≥f(x1)+f(x2)成立,则称f(x)为G函数.已知函数g(x)=x2与h(x)=a-2x-1是定义在[0,1]上的函数.
(1)试问函数g(x)是否为G函数?并说明理由;
(2)若函数h(x)是G函数,求实数a的值;
(3)在(2)的条件下,利用函数图象讨论方程g(2x)+h(-2x+1)=m(m∈R)解的个数情况.
查看习题详情和答案>>
(1)试问函数g(x)是否为G函数?并说明理由;
(2)若函数h(x)是G函数,求实数a的值;
(3)在(2)的条件下,利用函数图象讨论方程g(2x)+h(-2x+1)=m(m∈R)解的个数情况.
为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=
(0≤x≤10),若不建隔热层(即x=0时),每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(1)求k的值;
(2)求f(x)的表达式;
(3)利用“函数y=x+
(其中a为大于0的常数),在(0,
]上是减函数,在[
,+∞)上是增函数”这一性质,求隔热层修建多厚时,总费用f(x)达到最小,并求出这个最小值.
查看习题详情和答案>>
| k |
| 3x+5 |
(1)求k的值;
(2)求f(x)的表达式;
(3)利用“函数y=x+
| a |
| x |
| a |
| a |
我国农业科学家在某地区研究玉米植株生长与时间的函数关系,通过观测、分析,列出了该地区玉米在不同阶段的高度数据:
生长阶段 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
植株高度(cm) | 0.67 | 0.85 | 1.28 | 1.75 | 2.27 | 2.75 | 3.69 | 4.71 | 6.36 | 7.73 | 9.91 |
生长阶段 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
植株高度(cm) | 12.75 | 16.55 | 20.1 | 27.35 | 32.55 | 37.55 | 44.75 | 53.38 | 71.61 | 83.89 | 97.46 |
生长阶段 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
|
|
植株高度(cm) | 112.73 | 135.12 | 153.6 | 160.32 | 167.05 | 174.9 | 177.87 | 180.19 | 180.79 |
|
|
(1)画出函数图形,近似地写出一个函数关系式表达两个变量之间的关系;
(2)利用得出的关系式,与表中实际数据比较;
(3)说出关系式给出的一些信息.