题目内容
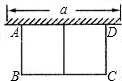 如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为Xm,面积为Sm2,
如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为Xm,面积为Sm2,(1)求S与X的函数关系式;
(2)如果要围成面积为45m2的花圃,AB的长是多少米?
(3)能围成面积比45m2更大的花圃吗?如果能,请求出最大面积.并说明围法;如果不能,请说明理由.
分析:(1)根据AB为xm,BC就为(24-3x),利用长方体的面积公式,可求出关系式.
(2)将s=45m代入(1)中关系式,可求出x即AB的长.
(3)当墙的宽度为最大时,有最大面积的花圃.此故可求.
(2)将s=45m代入(1)中关系式,可求出x即AB的长.
(3)当墙的宽度为最大时,有最大面积的花圃.此故可求.
解答:解:(1)根据题意,得S=x(24-3x),
即所求的函数解析式为:S=-3x2+24x,
又∵0<24-3x≤10,
∴定义域为
≤x<8;
(2)根据题意,设AB长为x,则BC长为24-3x
∴-3x2+24x=45.
整理,得x2-8x+15=0,
解得x=3或5,
当x=3时,BC=24-9=15>10不成立,
当x=5时,BC=24-15=9<10成立,
∴AB长为5m;
(3)S=24x-3x2=-3(x-4)2+48
∵墙的最大可用长度为10m,0≤BC=24-3x≤10,∴
≤x≤8,
∴x∈[
,8),因为对称轴x=4,开口向下,
∴当x=
m,有最大面积的花圃.
即:x=
m,
最大面积为:=24×
-3×(
)2=46.67m2
即所求的函数解析式为:S=-3x2+24x,
又∵0<24-3x≤10,
∴定义域为
| 14 |
| 3 |
(2)根据题意,设AB长为x,则BC长为24-3x
∴-3x2+24x=45.
整理,得x2-8x+15=0,
解得x=3或5,
当x=3时,BC=24-9=15>10不成立,
当x=5时,BC=24-15=9<10成立,
∴AB长为5m;
(3)S=24x-3x2=-3(x-4)2+48
∵墙的最大可用长度为10m,0≤BC=24-3x≤10,∴
| 14 |
| 3 |
∴x∈[
| 14 |
| 3 |
∴当x=
| 14 |
| 3 |
即:x=
| 14 |
| 3 |
最大面积为:=24×
| 14 |
| 3 |
| 14 |
| 3 |
点评:本题以实际问题为载体,主要考查了二次函数的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.本题的关键是垂直于墙的有三道篱笆.

练习册系列答案
相关题目
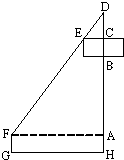 如图,在某建筑工地上有一个吊臂长DF=24m的吊车,吊车底座FG高1.m.现准备把一个底半径为3m、高2m的圆柱形工件吊起平放到15m高的桥墩上.(注:当物件与吊臂接触后,钢索CD长可通过顶点D处的滑轮自动调节并保持物件始终与吊臂接触,且与工件的中心在一条垂直线上.)
如图,在某建筑工地上有一个吊臂长DF=24m的吊车,吊车底座FG高1.m.现准备把一个底半径为3m、高2m的圆柱形工件吊起平放到15m高的桥墩上.(注:当物件与吊臂接触后,钢索CD长可通过顶点D处的滑轮自动调节并保持物件始终与吊臂接触,且与工件的中心在一条垂直线上.)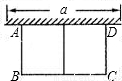 如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为Xm,面积为Sm2,
如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为Xm,面积为Sm2,