题目内容
我国农业科学家在某地区研究玉米植株生长与时间的函数关系,通过观测、分析,列出了该地区玉米在不同阶段的高度数据:生长阶段 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
植株高度(cm) | 0.67 | 0.85 | 1.28 | 1.75 | 2.27 | 2.75 | 3.69 | 4.71 | 6.36 | 7.73 | 9.91 |
生长阶段 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
植株高度(cm) | 12.75 | 16.55 | 20.1 | 27.35 | 32.55 | 37.55 | 44.75 | 53.38 | 71.61 | 83.89 | 97.46 |
生长阶段 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
|
|
植株高度(cm) | 112.73 | 135.12 | 153.6 | 160.32 | 167.05 | 174.9 | 177.87 | 180.19 | 180.79 |
|
|
(1)画出函数图形,近似地写出一个函数关系式表达两个变量之间的关系;
(2)利用得出的关系式,与表中实际数据比较;
(3)说出关系式给出的一些信息.
解析:指数函数、对数函数以及幂函数是描述客观变化规律的重要数学模型,本题通过画出函数图形,假设为指数函数,结合图表,可以清楚地看出,第1到第6个生长阶段与实际得到的数据误差很小,后面的数据误差较大.
解:(1)画出函数图形(如下图所示),函数的图形近似于“S”形.
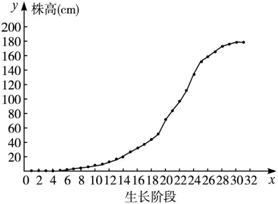
(2)以我们现有的知识很难找出一个函数关系式来近似地表达这个图形,但我们仔细观察第1个生长阶段至第25个生长阶段的函数图象后会发现,它与我们比较熟悉的指数函数的图象相像.
下面我们来考虑给出第1至第25个生长阶段的一个指数函数关系式.
假设指数函数为y=aebx,并且通过点(2,0.85)和(23,112.73),把这两个点的坐标代入函数关系式,解方程组得a=0.534,b=0.233.
因此,用指数函数近似得到的关系式为
y=f(x)=0.534e0.233x.
由得到的关系式计算出各个生长阶段的近似值如下表:
生长阶段x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |||||||||||
函数值f(x) | 0.67 | 0.85 | 1.07 | 1.36 | 1.71 | 2.16 | 2.73 | 3.44 | 4.34 | 5.48 | 6.92 | 8.74 | 11.03 | |||||||||||
生长阶段x | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | ||||||||||||
函数值f(x) | 13.93 | 17.58 | 22.2 | 28.02 | 35.37 | 44.66 | 56.37 | 71.16 | 89.84 | 113.41 | 143.17 | 180.73 | ||||||||||||
从表中我们可以清楚地看出,第1到第6个生长阶段与实际得到的数据误差很小,后面的数据误差较大.
(3)这个指数函数在玉米生长的后几个阶段增长较快,与实际数据中稳定于某一数值附近不符.

 阅读快车系列答案
阅读快车系列答案