摘要: 结合熟悉的具体函数.理解函数的单调性.最大(小)值及其几何意义.了解奇偶性和周期性的含义.通过具体函数的图象.初步了解中心对称图形和轴对称图形.
网址:http://m.1010jiajiao.com/timu_id_4460062[举报]
已知函数f(x)(x∈R)满足:对于任意实数x,y,都有f(x+y)=f(x)+f(y)+
恒成立,且当x>0时,f(x)>-
恒成立;
(1)求f(0)的值,并例举满足题设条件的一个特殊的具体函数;
(2)判定函数f(x)在R上的单调性,并加以证明;
(3)若函数F(x)=f(max{-x,2x-x2})+f(-k)+1(其中max{a,b}=
)有三个零点x1,x2,x3,求u=(x1+x2+x3)+x1•x2•x3的取值范围.
查看习题详情和答案>>
| 1 |
| 2 |
| 1 |
| 2 |
(1)求f(0)的值,并例举满足题设条件的一个特殊的具体函数;
(2)判定函数f(x)在R上的单调性,并加以证明;
(3)若函数F(x)=f(max{-x,2x-x2})+f(-k)+1(其中max{a,b}=
|
函数f(x)满足:(1)定义域是(0,+∞);(2)当x>1时,f(x)<2;(3)对任意x,y∈(0,+∞),总有f(xy)=f(x)+f(y)-2.则
(1)求出f(1)的值;
(2)写出一个满足上述条件的具体函数;
(3)判断函数f(x)的单调性,并用定义加以证明. 查看习题详情和答案>>
(1)求出f(1)的值;
(2)写出一个满足上述条件的具体函数;
(3)判断函数f(x)的单调性,并用定义加以证明. 查看习题详情和答案>>
函数f(x)满足:①定义域是(0,+∞) ②当x>1时,f(x)<2;③对任意x,y∈(0,+∞),总有f(xy)=f(x)+f(y)-2
(1)求出f(1)的值;
(2)判断函数f(x)的单调性,并用单调性的定义证明你的结论;
(3)写出一个满足上述条件的具体函数.
查看习题详情和答案>>
(1)求出f(1)的值;
(2)判断函数f(x)的单调性,并用单调性的定义证明你的结论;
(3)写出一个满足上述条件的具体函数.
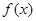 满足:①定义域是
满足:①定义域是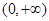 ; ②当
; ②当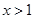 时,
时,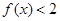 ;
; ,总有
,总有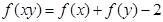
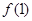 的值;
的值;