题目内容
函数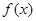 满足:①定义域是
满足:①定义域是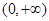 ; ②当
; ②当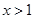 时,
时,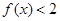 ;
;
③对任意 ,总有
,总有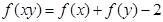
(1)求出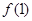 的值;
的值;
(2)判断函数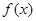 的单调性,并用单调性的定义证明你的结论;
的单调性,并用单调性的定义证明你的结论;
(3)写出一个满足上述条件的具体函数。
【答案】
解:(1)令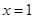 ,有
,有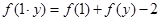 ,
,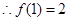
(2) 在
在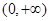 单调递减
单调递减
事实上,设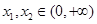 ,且
,且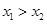 ,则
,则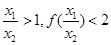
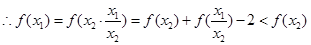 ,
,
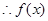 在
在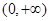 上单调递减
上单调递减
(3)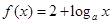 ,其中
,其中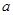 可以取
可以取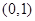 内的任意一个实数
内的任意一个实数
【解析】略

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目