摘要：将 y=12代入(1)得: x=23 所以 答:鸡有23只.兔有12只. 22. 解: .得.即. ----------------------------3分 把代入(1).得. ------------------------------5分 ∴ 原方程组的解为: ----------------------------6分 (用代入消元法.同理给分)
网址：http://m.1010jiajiao.com/timu_id_4459451[举报]
阅读材料，解答问题．
材料：利用解二元一次方程组的代入消元法可解形如
的方程组．
如：由（2）得y=x-1，代入（1）消元得到关于x的方程：x2-x+
=0，∴x1=x2=
将x1=x2=
代入y=x-1得y1=y2=-
，∴方程组的解为
．
请你用代入消元法解方程组
．
查看习题详情和答案>>
材料：利用解二元一次方程组的代入消元法可解形如
|
如：由（2）得y=x-1，代入（1）消元得到关于x的方程：x2-x+
| 1 |
| 4 |
| 1 |
| 2 |
将x1=x2=
| 1 |
| 2 |
| 1 |
| 2 |
|
请你用代入消元法解方程组
|
阅读下列范例，按要求解答问题．
例：已知实数a、b、c满足a+b+2c=1，a2+b2+6c+
=0，求a、b、c的值．
解法1：由已知得a+b=1-2c，①（a+b）2-2ab+6c+
=0．②
将①代入②，整理得4c2+2c-2ab+
=0．∴ab=2c2+c+
③
由①、③可知，a、b是关于t的方程t2-（1-2c）t+2c2+c+
=0④的两个实数根．
∴△=（1-2c）2-4（2c2+c+
≥0，即（c+1）2≤0．而（c+1）2≥0，∴c+l=0，c=-1，
将c=-1代入④，得t2-3t+
=0．∴t1=t2=
，即a=b=
．∴a=b，c=-1．
解法2∵a+b+2c=1，∴a+b=1-2c、设a=
+t，b=
-t．①
∵a2+b2+6c+
=0，∴（a+b）2-2ab+6c+
=0．②
将①代入②，得（1-2c）2-2(
+t)(
-t)+6c+
=0．
整理，得t2+（c2+2c+1）=0，即t2+（c+1）2=0．∴t=0，c=-1．
将t、c的值同时代入①，得a=
，b=
．a=b=
，c=-1．
以上解法1是构造一元二次方程解决问题．若两实数x、y满足x+y=m，xy=n，则x、y是关于t的一元二次方程t2-mt+n=0的两个实数根，然后利用判别式求解．
以上解法2是采用均值换元解决问题．若实数x、y满足x+y=m，则可设x=
+t，y=
-t．一些问题根据条件，若合理运用这种换元技巧，则能使问题顺利解决．
下面给出两个问题，解答其中任意一题：
（1）用另一种方法解答范例中的问题．
（2）选用范例中的一种方法解答下列问题：
已知实数a、b、c满足a+b+c=6，a2+b2+c2=12，求证：a=b=c． 查看习题详情和答案>>
例：已知实数a、b、c满足a+b+2c=1，a2+b2+6c+
| 3 |
| 2 |
解法1：由已知得a+b=1-2c，①（a+b）2-2ab+6c+
| 3 |
| 2 |
将①代入②，整理得4c2+2c-2ab+
| 5 |
| 2 |
| 5 |
| 4 |
由①、③可知，a、b是关于t的方程t2-（1-2c）t+2c2+c+
| 5 |
| 4 |
∴△=（1-2c）2-4（2c2+c+
| 5 |
| 4 |
将c=-1代入④，得t2-3t+
| 9 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
解法2∵a+b+2c=1，∴a+b=1-2c、设a=
| 1-2c |
| 2 |
| 1-2c |
| 2 |
∵a2+b2+6c+
| 3 |
| 2 |
| 3 |
| 2 |
将①代入②，得（1-2c）2-2(
| 1-2c |
| 2 |
| 1-2c |
| 2 |
| 3 |
| 2 |
整理，得t2+（c2+2c+1）=0，即t2+（c+1）2=0．∴t=0，c=-1．
将t、c的值同时代入①，得a=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
以上解法1是构造一元二次方程解决问题．若两实数x、y满足x+y=m，xy=n，则x、y是关于t的一元二次方程t2-mt+n=0的两个实数根，然后利用判别式求解．
以上解法2是采用均值换元解决问题．若实数x、y满足x+y=m，则可设x=
| m |
| 2 |
| m |
| 2 |
下面给出两个问题，解答其中任意一题：
（1）用另一种方法解答范例中的问题．
（2）选用范例中的一种方法解答下列问题：
已知实数a、b、c满足a+b+c=6，a2+b2+c2=12，求证：a=b=c． 查看习题详情和答案>>
如图，矩形ABCD中，E为BC上一点，DF⊥AE于F.(1)ΔABE与ΔADF相似吗？请说明理由.(2)若AB=6，AD=12，BE=8，求DF的长.
【解析】（1）根据矩形的性质和DF⊥AE，可得∠ABE=∠AFD=90°，∠AEB=∠DAF，即可证明△ABE∽△ADF．
（2）利用△ABE∽△ADF，得
，再利用勾股定理，求出AE的长，然后将已知数值代入即可求出DF的长
查看习题详情和答案>>
（2002•荆门）阅读下列范例，按要求解答问题．
例：已知实数a、b、c满足a+b+2c=1，a2+b2+6c+
=0，求a、b、c的值．
解法1：由已知得a+b=1-2c，①（a+b）2-2ab+6c+
=0．②
将①代入②，整理得4c2+2c-2ab+
=0．∴ab=2c2+c+
③
由①、③可知，a、b是关于t的方程t2-（1-2c）t+2c2+c+
=0④的两个实数根．
∴△=（1-2c）2-4（2c2+c+
≥0，即（c+1）2≤0．而（c+1）2≥0，∴c+l=0，c=-1，
将c=-1代入④，得t2-3t+
=0．∴t1=t2=
，即a=b=
．∴a=b，c=-1．
解法2∵a+b+2c=1，∴a+b=1-2c、设a=
+t，b=
-t．①
∵a2+b2+6c+
=0，∴（a+b）2-2ab+6c+
=0．②
将①代入②，得（1-2c）2-2
+6c+
=0．
整理，得t2+（c2+2c+1）=0，即t2+（c+1）2=0．∴t=0，c=-1．
将t、c的值同时代入①，得a=
，b=
．a=b=
，c=-1．
以上解法1是构造一元二次方程解决问题．若两实数x、y满足x+y=m，xy=n，则x、y是关于t的一元二次方程t2-mt+n=0的两个实数根，然后利用判别式求解．
以上解法2是采用均值换元解决问题．若实数x、y满足x+y=m，则可设x=
+t，y=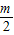
-t．一些问题根据条件，若合理运用这种换元技巧，则能使问题顺利解决．
下面给出两个问题，解答其中任意一题：
（1）用另一种方法解答范例中的问题．
（2）选用范例中的一种方法解答下列问题：
已知实数a、b、c满足a+b+c=6，a2+b2+c2=12，求证：a=b=c．
查看习题详情和答案>>
例：已知实数a、b、c满足a+b+2c=1，a2+b2+6c+
=0，求a、b、c的值．解法1：由已知得a+b=1-2c，①（a+b）2-2ab+6c+
=0．②将①代入②，整理得4c2+2c-2ab+
=0．∴ab=2c2+c+③由①、③可知，a、b是关于t的方程t2-（1-2c）t+2c2+c+
=0④的两个实数根．∴△=（1-2c）2-4（2c2+c+
≥0，即（c+1）2≤0．而（c+1）2≥0，∴c+l=0，c=-1，将c=-1代入④，得t2-3t+
=0．∴t1=t2=，即a=b=．∴a=b，c=-1．解法2∵a+b+2c=1，∴a+b=1-2c、设a=
+t，b=-t．①∵a2+b2+6c+
=0，∴（a+b）2-2ab+6c+=0．②将①代入②，得（1-2c）2-2
+6c+=0．整理，得t2+（c2+2c+1）=0，即t2+（c+1）2=0．∴t=0，c=-1．
将t、c的值同时代入①，得a=
，b=．a=b=，c=-1．以上解法1是构造一元二次方程解决问题．若两实数x、y满足x+y=m，xy=n，则x、y是关于t的一元二次方程t2-mt+n=0的两个实数根，然后利用判别式求解．
以上解法2是采用均值换元解决问题．若实数x、y满足x+y=m，则可设x=
+t，y=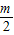-t．一些问题根据条件，若合理运用这种换元技巧，则能使问题顺利解决．下面给出两个问题，解答其中任意一题：
（1）用另一种方法解答范例中的问题．
（2）选用范例中的一种方法解答下列问题：
已知实数a、b、c满足a+b+c=6，a2+b2+c2=12，求证：a=b=c．
查看习题详情和答案>>