摘要：立足中下题目.力争高水平 平时做作业.都是按所有题目来完成的.但高考却不然.只有个别的同学能交满分卷.因为时间和个别题目的难度都不允许多数学生去做完.做对全部题目.所以在答卷中要立足中下题目.中下题目通常占全卷的80%以上.是试题的主要构成.是考生得分的主要来源.学生能拿下这些题目.实际上就是数学科打了个胜仗.有了胜利在握的心理.对攻克高档题会更放得开.
网址：http://m.1010jiajiao.com/timu_id_4457792[举报]
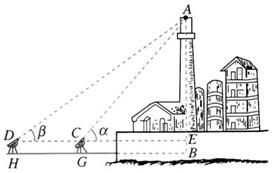
（2012•荆州模拟）OP是底部O不能到达的高塔，P是高塔的最高点，选择一条水平基线M，N，使得M，N，O三点在同一条直线上，在相距为d的M，N两点用测角仪测得P的仰角分别为α，β，已知测角仪高h=1.5m，试完成如下《实验报告》
（要求：（1）计算两次测量值的平均值并填入表格；（2）利用α，β，d的平均值，求OP的值，写出详细的计算过程；
（3）把计算结果填入表格．（相关数据：）
查看习题详情和答案>>
（要求：（1）计算两次测量值的平均值并填入表格；（2）利用α，β，d的平均值，求OP的值，写出详细的计算过程；
（3）把计算结果填入表格．（相关数据：）
| 题目 | 测量底部不能到达的高塔的高度 | 计算过程 | |||
| 测量数据 | 测量项目 | 第一次 | 第二次 | 平均值 | |
| α | 75°32′ | 74°28′ | |||
| β | 30°17′ | 29°43′ | |||
| d（m） | 59.82 | 60.18 | |||
| 测量目标 | |||||
| 结果 | |||||
足球射门与概率
如果你是一名足球运动员,在足球比赛中若遇到罚点球射门时,这时若要罚进不仅仅要靠运气,还要靠智慧的头脑.首先假设不存在射飞或射高的情况.在扑对方向的前提下守门员也不会失误或脱手,也不考虑补射的情况(点球大战中根本不存在).就是说球只有两种状态:射进或被扑出.球员射门有6个方向:中下,中上,左下,右下,左上,右上.而作为守门员,扑球有5种选择:不动,左下,右下,左上,右上.
若①不动可扑出中下和中上两个方向的点球;
②左下可扑出左下和中下;
③右下可扑出右下和中下;
④左上可扑出左上;
⑤右上可扑出右上.
你会用你智慧的大脑运用概率的知识选择射门的方向吗？
查看习题详情和答案>>
OP是底部O不能到达的高塔，P是高塔的最高点，选择一条水平基线M，N，使得M，N，O三点在同一条直线上，在相距为d的M，N两点用测角仪测得P的仰角分别为α，β，已知测角仪高h=1.5m，试完成如下《实验报告》
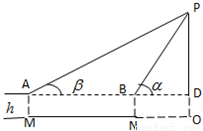
（要求：（1）计算两次测量值的平均值并填入表格；（2）利用α，β，d的平均值，求OP的值，写出详细的计算过程；
（3）把计算结果填入表格．（相关数据：）
查看习题详情和答案>>
（要求：（1）计算两次测量值的平均值并填入表格；（2）利用α，β，d的平均值，求OP的值，写出详细的计算过程；
（3）把计算结果填入表格．（相关数据：）
| 题目 | 测量底部不能到达的高塔的高度 | 计算过程 | |||
| 测量数据 | 测量项目 | 第一次 | 第二次 | 平均值 | |
| α | 75°32′ | 74°28′ | |||
| β | 30°17′ | 29°43′ | |||
| d（m） | 59.82 | 60.18 | |||
| 测量目标 | |||||
| 结果 | |||||
查看习题详情和答案>>
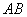是底部
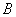不能到达的烟囱，
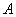是烟囱的最高点，选择一条水平基线
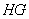，使得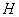
、
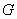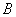、三点在同一条直线上，在相距为
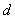的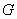、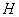两点用测角仪测得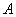的仰角分别为
、
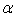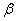，已知测角仪器高
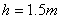，试完成如下《实验报告》（要求：1. 计算两次测量值的平均值,填入表格；2. 利用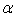、、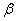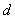的平均值，求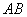的值，写出详细计算过程；3. 把计算
结果填入表格） 相关数据：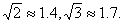
|
题目 |
测量底部不能到达的烟囱的高 |
计算过程 |
|||
|
测 量 数 据 |
测量项目 |
第一次 |
第二次 |
平均值 |
|
|
|
74°52' |
75°8' |
|
||
|
|
30°12' |
29°48' |
|
||
|
|
59.78 |
60.22 |
|
||
|
测量目标 （附图） |
|
||||
|
结果 |
|
)
查看习题详情和答案>>
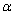
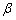
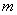