摘要:在平面直角坐标系中,ΔAOB的位置如图所示,已知∠AOB=90°,AO=BO,点A的坐标为. (1)求点B的坐标; (2)求过A.O.B三点的抛物线的解析式; (3) 抛物线的对称轴上有一点M,且点M的纵坐标与点B的纵坐标相等,连结AM.BM.求ΔAMB的面积. 解:(1)过点A作AC⊥x轴于点C, 过点B作BD⊥x轴于点D, ∵ ∠AOB=90°, ∴ ∠AOC=∠OBD ∵ ∠ACO=∠ODB=90°, AO=BO ∴ΔACO≌ΔODB ∴OD=CA=1,BD=CO=3 ∴点B的坐标为(1,3). (2)设函数解析式为y=ax2+bx(a≠0) 可得 9a-3b=1 a+b=3 解得: 此解析式为 (3)解得对称轴 x=- ∴ M点坐标为( - ,3) 则BM=|1 –(-)| = MB边上的高=|3-1|=2 ΔABM的面积=2×÷ 2=
网址:http://m.1010jiajiao.com/timu_id_4455346[举报]
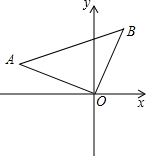
在平面直角坐标系中,△AOB的位置如图所示,已知∠AOB=90°,AO=BO,点A的坐标为(-3 ,1).
,1).
(1)求点B的坐标;
(2)求过A,O,B三点的抛物线的解析式;
(3)设点B关于抛物线的对称轴l的对称点为B1,求△AB1B的面积. 查看习题详情和答案>>
 ,1).
,1).(1)求点B的坐标;
(2)求过A,O,B三点的抛物线的解析式;
(3)设点B关于抛物线的对称轴l的对称点为B1,求△AB1B的面积. 查看习题详情和答案>>
在平面直角坐标系中有一点A(
,-
),过A点作x轴的平行线l,在l上有一不与A点重合的点B,连接OA,OB.将OA绕O点顺时针方向旋转α°到OA1,OB绕O点逆时针方向旋转α°到OB1.
(1)当B点在A点右侧时,如图(1).如果∠AOB=20°,∠A1OB=110°,α= .这时直线AB1与直线A1B有何特殊的位置关系证明你的结论.
(2)如果B点的横坐标为t,△OAB的面积为S,直接写出S关于t的函数关式,并指出t的取值范围.
(3)当α=60时,直线B1A交y轴于D,求以D为顶点且经过A点的抛物线的解析式.
 查看习题详情和答案>>
查看习题详情和答案>>
| 1 |
| 2 |
| ||
| 2 |
(1)当B点在A点右侧时,如图(1).如果∠AOB=20°,∠A1OB=110°,α=
(2)如果B点的横坐标为t,△OAB的面积为S,直接写出S关于t的函数关式,并指出t的取值范围.
(3)当α=60时,直线B1A交y轴于D,求以D为顶点且经过A点的抛物线的解析式.
 查看习题详情和答案>>
查看习题详情和答案>>
在平面直角坐标系中,放置一个如图所示的直角三角形纸片AOB,已知OA=2,∠AOB=30度.D、E两点同时从原点O出发,D点以每秒
个单位长度的速度沿x轴正方向运动,E点以每秒1个单位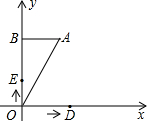 长度的速度沿y轴正方向运动,设D、E两点的运动时间为t秒.
长度的速度沿y轴正方向运动,设D、E两点的运动时间为t秒.
(1)点A的坐标为 ,点B的坐标为 ;
(2)在点D、E的运动过程中,直线DE与直线OA垂直吗?请说明理由;
(3)当时间t在什么范围时,直线DE与线段OA有公共点?
(4)将直角三角形纸片AOB在直线DE下方的部分沿DE向上折叠,设折叠后重叠部分面积为S,请写出S与t的函数关系式,并求出S的最大值. 查看习题详情和答案>>
| 3 |
 长度的速度沿y轴正方向运动,设D、E两点的运动时间为t秒.
长度的速度沿y轴正方向运动,设D、E两点的运动时间为t秒.(1)点A的坐标为
(2)在点D、E的运动过程中,直线DE与直线OA垂直吗?请说明理由;
(3)当时间t在什么范围时,直线DE与线段OA有公共点?
(4)将直角三角形纸片AOB在直线DE下方的部分沿DE向上折叠,设折叠后重叠部分面积为S,请写出S与t的函数关系式,并求出S的最大值. 查看习题详情和答案>>
 ,1).
,1). .
.