题目内容
在平面直角坐标系中,放置一个如图所示的直角三角形纸片AOB,已知OA=2,∠AOB=30度.D、E两点同时从原点O出发,D点以每秒| 3 |
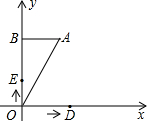 长度的速度沿y轴正方向运动,设D、E两点的运动时间为t秒.
长度的速度沿y轴正方向运动,设D、E两点的运动时间为t秒.(1)点A的坐标为
(2)在点D、E的运动过程中,直线DE与直线OA垂直吗?请说明理由;
(3)当时间t在什么范围时,直线DE与线段OA有公共点?
(4)将直角三角形纸片AOB在直线DE下方的部分沿DE向上折叠,设折叠后重叠部分面积为S,请写出S与t的函数关系式,并求出S的最大值.
分析:(1)由题意可知:OA=2,∠AOB=30°,则根据直角三角形中30°所对的边是斜边的一半,则AB=1,根据勾股定理可以求得OB=
;所以可以求得点A与点B的坐标.
(2)如果连接DE,那么根据D、E两点的速度可得出OD:OE=
,因此直角三角形ODE中,∠OED=60°,而已知了∠AOB=30°,即可得出OA⊥DE.
(3)本题只需考查直线DE过O,A两点时,t的取值即可.
(4)本题要分三种情况进行讨论.
①当0≤t≤
时,重合部分是三角形.
②当
<t≤
时,重合部分是四边形.
③当
<t≤
时,重合部分是三角形.
可据此来求出S,t的关系式,以及S的最大取值.
| 3 |
(2)如果连接DE,那么根据D、E两点的速度可得出OD:OE=
| 3 |
(3)本题只需考查直线DE过O,A两点时,t的取值即可.
(4)本题要分三种情况进行讨论.
①当0≤t≤
2
| ||
| 3 |
②当
2
| ||
| 3 |
| 3 |
③当
| 3 |
4
| ||
| 3 |
可据此来求出S,t的关系式,以及S的最大取值.
解答: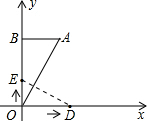 解:(1)由题意可知:OA=2,∠AOB=30°,则根据直角三角形中30°所对的边是斜边的一半,则AB=1,根据勾股定理可以求得OB=
解:(1)由题意可知:OA=2,∠AOB=30°,则根据直角三角形中30°所对的边是斜边的一半,则AB=1,根据勾股定理可以求得OB=
;则点A的坐标为(1,
),点B的坐标为(0,
);
(2)垂直.
理由:连接DE,直角三角形ODE中,tan∠OED=
=
,
∴∠OED=60°.
∵∠BOA=30°,
∴OA⊥ED.
(3)因为DE总是垂直于OA运动,因此可以看做直线DE沿OA方向进行运动.因此两者有公共点的取值范围就是O?A之间.
当DE过O点时,t=0.
当DE过A点时,直角三角形OAD中,OA=2,∠ODA=30°,因此OD=4,t=
.
因此t的取值范围是0≤t≤
.
(4)当0≤t≤
时,S=
t2;Smax=
;
当
<t≤
时,S=
-
t2-
(
-t)2=-
(t-
)2+
,Smax=
;
当
<t≤
时,S=
(2-
t)2,S无最大值;
综上所述S的最大值为
.
 解:(1)由题意可知:OA=2,∠AOB=30°,则根据直角三角形中30°所对的边是斜边的一半,则AB=1,根据勾股定理可以求得OB=
解:(1)由题意可知:OA=2,∠AOB=30°,则根据直角三角形中30°所对的边是斜边的一半,则AB=1,根据勾股定理可以求得OB=| 3 |
| 3 |
| 3 |
(2)垂直.
理由:连接DE,直角三角形ODE中,tan∠OED=
| OD |
| OE |
| 3 |
∴∠OED=60°.
∵∠BOA=30°,
∴OA⊥ED.
(3)因为DE总是垂直于OA运动,因此可以看做直线DE沿OA方向进行运动.因此两者有公共点的取值范围就是O?A之间.
当DE过O点时,t=0.
当DE过A点时,直角三角形OAD中,OA=2,∠ODA=30°,因此OD=4,t=
4
| ||
| 3 |
因此t的取值范围是0≤t≤
4
| ||
| 3 |
(4)当0≤t≤
2
| ||
| 3 |
| ||
| 8 |
| ||
| 6 |
当
2
| ||
| 3 |
| 3 |
| ||
| 2 |
| ||
| 8 |
| ||
| 2 |
| 3 |
5
| ||
| 8 |
4
| ||
| 5 |
| ||
| 5 |
| ||
| 5 |
当
| 3 |
4
| ||
| 3 |
| ||
| 2 |
| ||
| 2 |
综上所述S的最大值为
| ||
| 5 |
点评:本题中对于点的运动要分类进行讨论.分类讨论是初中数学重要的思想方法,难点是一要想到用讨论的方法进行求解.二是讨论界限要确定不要漏解和重复.

练习册系列答案
相关题目
 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB= 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.