题目内容
在平面直角坐标系中,△AOB的位置如图所示.已知∠AOB=90°,AO=BO,点A的坐标为(-3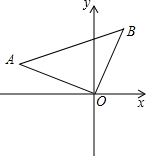 ,1).
,1).(1)求点B的坐标.
(2)求过A,O,B三点的抛物线的解析式.
(3)设点B关于抛物线的对称轴?的对称点为Bl,连接AB1,求tan∠AB1B的值.
分析:(1)作辅助线,构造直角,在直角三角形中解题,证三角形全等,从而求得B点坐标;
(2)求解析式已知两定点,用待定系数求出解析式;
(3)写出对称轴方程,由点关于直线对称,求出对称点,从而可求tan∠AB1B的值.
(2)求解析式已知两定点,用待定系数求出解析式;
(3)写出对称轴方程,由点关于直线对称,求出对称点,从而可求tan∠AB1B的值.
解答: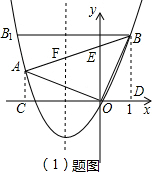 解:(1)作AC⊥x轴,BD⊥x轴,垂足分别为C,D,(2分)
解:(1)作AC⊥x轴,BD⊥x轴,垂足分别为C,D,(2分)
则∠ACO=∠ODB=90°.
∴∠AOC+∠OAC=90°.
又∵∠AOB=90°,
∴∠AOC+∠BOD=90°.
∴∠OAC=∠BOD.
又∵AO=BO,
∴△ACO≌△ODB.(5分)
∴OD=AC=1,DB=OC=3.
∴点B的坐标为(1,3).(7分)
(2)抛物线过原点,可设所求抛物线的解析式为y=ax2+bx.
将A(-3,1),B(1,3)代入,
得
,
解得a=
,b=
故所求抛物线的解析式为y=
x2+
x.(10分)
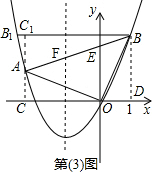
(3)抛物线y=
x2+
x的对称轴l的方程是x=-
=-
.
点B关于抛物线的对称轴l的对称点为B1(-
,3).(12分)
在△AB1B中,作AC1⊥BBl于C1,
则C1(-3,3),BlC1=
,AC1=2.
∴tan∠AB1B=
.(14分)
 解:(1)作AC⊥x轴,BD⊥x轴,垂足分别为C,D,(2分)
解:(1)作AC⊥x轴,BD⊥x轴,垂足分别为C,D,(2分)则∠ACO=∠ODB=90°.
∴∠AOC+∠OAC=90°.
又∵∠AOB=90°,
∴∠AOC+∠BOD=90°.
∴∠OAC=∠BOD.
又∵AO=BO,
∴△ACO≌△ODB.(5分)
∴OD=AC=1,DB=OC=3.
∴点B的坐标为(1,3).(7分)
(2)抛物线过原点,可设所求抛物线的解析式为y=ax2+bx.
将A(-3,1),B(1,3)代入,
得
|
解得a=
| 5 |
| 6 |
| 13 |
| 6 |
故所求抛物线的解析式为y=
| 5 |
| 6 |
| 13 |
| 6 |

(3)抛物线y=
| 5 |
| 6 |
| 13 |
| 6 |
| b |
| 2a |
| 13 |
| 10 |
点B关于抛物线的对称轴l的对称点为B1(-
| 18 |
| 5 |
在△AB1B中,作AC1⊥BBl于C1,
则C1(-3,3),BlC1=
| 3 |
| 5 |
∴tan∠AB1B=
| 10 |
| 3 |
点评:此题考查直角三角形的性质及函数的性质,待定系数法求抛物线解析式,还有点关于直线对称的问题,知识点多,但不难.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB= 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.