摘要：2．如图.在平行四边形ABCD中.过点B作BE⊥CD.垂足为E. 连结AE.F为AE上一点.且∠BFE＝∠C. (1)求证:△ABF∽△EAD. (2)若AB＝4.∠1＝30°.AD＝3.求BF的长． 解:(1)证明:∵AB∥CD.∴∠1＝∠2. 又∵∠BFE＝∠C.∠BFE+∠BFA＝∠C+∠EDA ∴∠BFA＝∠ADE.∴△ABF∽△EAD. (2)在Rt△ABE中.∠1＝30°. 由正弦定理得:＝. ∴AE＝＝. 又＝.∴BF＝·AD＝.
网址：http://m.1010jiajiao.com/timu_id_4453883[举报]
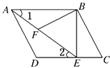如图，在平行四边形ABCD中，过点B作BE⊥CD，垂足为E，连接AE，F为AE上一点，且∠BFE=∠C．（1）求证：△ABF∽△EAD．
（2）若AB=4，∠1=30°，AD=3，求BF的长． 查看习题详情和答案>>
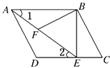如图，在平行四边形ABCD中，过点B作BE⊥CD，垂足为E，连接AE，F为AE上一点，且∠BFE=∠C．
（1）求证：△ABF∽△EAD．
（2）若AB=4，∠1=30°，AD=3，求BF的长．
查看习题详情和答案>>
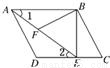
如图，在平行四边形ABCD中，过点B作BE⊥CD，垂足为E，连接AE，F为AE上一点，且∠BFE=∠C．
（1）求证：△ABF∽△EAD．
（2）若AB=4，∠1=30°，AD=3，求BF的长．
查看习题详情和答案>>
（1）求证：△ABF∽△EAD．
（2）若AB=4，∠1=30°，AD=3，求BF的长．
查看习题详情和答案>>
如图示，已知平行四边形ABCD和矩形ACEF所在平面互相垂直，AB=1，AD=2，∠ADC=60°，AF=1，M是线段EF的中点．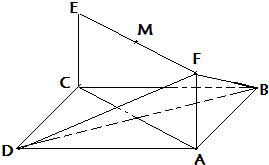
如图示，已知平行四边形ABCD和矩形ACEF所在平面互相垂直，AB=1，AD=2，∠ADC=60°，AF=1，M是线段EF的中点．