题目内容
如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠BFE=∠C.(1)求证:△ABF∽△EAD.
(2)若AB=4,∠1=30°,AD=3,求BF的长.
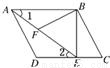
【答案】分析:(1)欲证:△ABF∽△EAD,根据相似三角形的判定,只须证明它们的两对对应角相等即可,由平行可得∠1=∠2,再根据:“∠BFE=∠C”结合平角相等,再证得:∠BFA=∠ADE即可;
(2)在Rt△ABE中,利用已恬角:∠1=30°,再由正弦定理得即可求得BF的长.
解答:解:(1)证明:∵AB∥CD,∴∠1=∠2,
又∵∠BFE=∠C,∠BFE+∠BFA=∠C+∠EDA
∴∠BFA=∠ADE,∴△ABF∽△EAD.
(2)在Rt△ABE中,∠1=30°,
由正弦定理得: =
= ,
,
∴AE=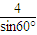 =
=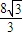 ,
,
又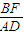 =
=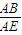 ,∴BF=
,∴BF=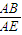 •AD=
•AD=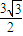 .
.
点评:本小题主要考查相似三角形的判定、正弦定理的应用等基础知识,考查运算求解能力.属于基础题.
(2)在Rt△ABE中,利用已恬角:∠1=30°,再由正弦定理得即可求得BF的长.
解答:解:(1)证明:∵AB∥CD,∴∠1=∠2,
又∵∠BFE=∠C,∠BFE+∠BFA=∠C+∠EDA
∴∠BFA=∠ADE,∴△ABF∽△EAD.
(2)在Rt△ABE中,∠1=30°,
由正弦定理得:
 =
= ,
,∴AE=
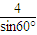 =
=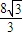 ,
,又
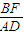 =
=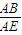 ,∴BF=
,∴BF=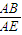 •AD=
•AD=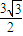 .
.点评:本小题主要考查相似三角形的判定、正弦定理的应用等基础知识,考查运算求解能力.属于基础题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 如图,在平行四边形ABCD中,下列结论中错误的是( )
如图,在平行四边形ABCD中,下列结论中错误的是( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
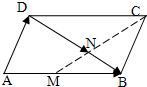 如图,在平行四边形ABCD,
如图,在平行四边形ABCD, 如图,在平行四边形ABCD中,
如图,在平行四边形ABCD中,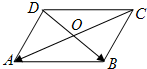 如图,在平行四边形ABCD中,若
如图,在平行四边形ABCD中,若 如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的中点.
如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的中点.