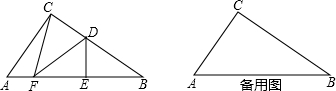
摘要：24． 已知:如图.C为BE上一点.点A.D分别在BE的两侧．AB//ED.AB=CE. BC=ED．试猜AC与CD有怎样的数量关系?并加以说明．
网址：http://m.1010jiajiao.com/timu_id_4452348[举报]
已知：如图1，在DE上取一点A，以AD、AE为正方形的一边在同一侧作正方形ABCD和正方形AEFG，连接DG、BE，则线段DG、BE之间满足DG=BE且DG⊥BE；
根据所给图形完成以下问题的探索、证明和计算：
（1）如图2，将正方形AEFG绕A点顺时针旋转α度，即∠BAG=α （0°＜α＜180°），那么（1）中的结论是否仍成立？若不成立请说明理由，若成立请给出证明．
（2）设正方形ABCD、AEFG的边长分别是3和2，线段BD、DE、EG、GB所围成封闭图形的面积为S．当α变化时，S是否有最大值？若有，求出S的最大值及相应的α值．
查看习题详情和答案>>
根据所给图形完成以下问题的探索、证明和计算：
（1）如图2，将正方形AEFG绕A点顺时针旋转α度，即∠BAG=α （0°＜α＜180°），那么（1）中的结论是否仍成立？若不成立请说明理由，若成立请给出证明．
（2）设正方形ABCD、AEFG的边长分别是3和2，线段BD、DE、EG、GB所围成封闭图形的面积为S．当α变化时，S是否有最大值？若有，求出S的最大值及相应的α值．
查看习题详情和答案>>
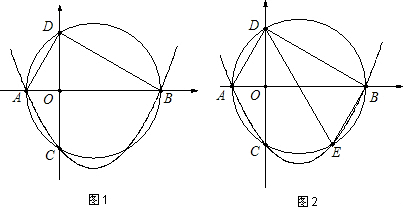
已知：抛物线y=ax2+bx+c的对称轴为x=
且经过点C（0，-3）和点F（3，-2
）．
（1）求抛物线的解析式：
（2）如图1，设抛物线y=ax2+bx+c与x 轴交于A、B两点，与y 轴交于点C，过A、B、C三点的⊙M交y 轴于另一点D，连接AD、DB，设∠CDB=α，∠ADC=β，求cos（α-β）的值；
（3）如图2，作∠CDB的平分线DE交⊙M于点E，连接BE，问：在坐标轴上是否存在点P，使得以P、D、E为顶点的三角形与△DEB相似．若存在，求出所有满足条件的点P的坐标（不包括点B）；若不存在，请说明理由．
查看习题详情和答案>>
| 3 |
| 3 |
（1）求抛物线的解析式：
（2）如图1，设抛物线y=ax2+bx+c与x 轴交于A、B两点，与y 轴交于点C，过A、B、C三点的⊙M交y 轴于另一点D，连接AD、DB，设∠CDB=α，∠ADC=β，求cos（α-β）的值；
（3）如图2，作∠CDB的平分线DE交⊙M于点E，连接BE，问：在坐标轴上是否存在点P，使得以P、D、E为顶点的三角形与△DEB相似．若存在，求出所有满足条件的点P的坐标（不包括点B）；若不存在，请说明理由．
查看习题详情和答案>>
如图，已知直线l1∥l2，线段AB在直线l1上，BC垂直于l1交l2于点C，且AB=BC，P是线段BC上异于两端点的一点，过点P的直线分别交l2、l1于点D、E（点A、E位于点B的两侧），满足BP=BE，连接AP、CE．
（1）求证：△ABP≌△CBE；
（2）连结AD、BD，BD与AP相交于点F．如图2．
①当
=2时，求证：AP⊥BD；
②当=n（n＞1）时，设△PAD的面积为S1，△PCE的面积为S2，求
的值．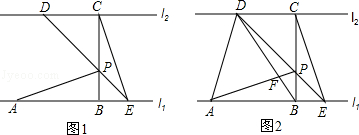
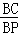=2时，求证：AP⊥BD；
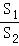的值．
：
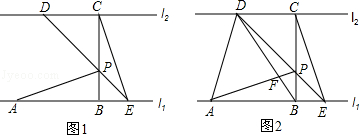
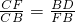．当DF⊥CF时，求BD的长．