摘要: 解:(Ⅰ)证明:CD//C1B1.又BD=BC=B1C1.∴ 四边形BDB1C1是平行四边形. ∴BC1//DB1.又DB1平面AB1D.BC1平面AB1D.∴直线BC1//平面AB1D. (Ⅱ)解:过B作BE⊥AD于E.连结EB1.∵B1B⊥平面ABD.∴B1E⊥AD . ∴∠B1EB是二面角B1-AD-B的平面角.∵BD=BC=AB.∴E是AD的中点. 在Rt△B1BE中. ∴∠B1EB=60°.即二面角B1-AD-B的大小为60°
网址:http://m.1010jiajiao.com/timu_id_4450416[举报]
 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)A.(选修4-4坐标系与参数方程)将参数方程
|
B.(选修4-5 不等式选讲)不等式|x-1|+|2x+3|>5的解集是
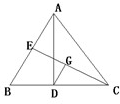
C.(选修4-1 几何证明选讲)如图,在△ABC中,AD是高线,CE是中线,|DC|=|BE|,DG⊥CE于G,且|EC|=8,则|EG|=
 A.(选修4-4坐标系与参数方程)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线ρsin(θ+
A.(选修4-4坐标系与参数方程)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线ρsin(θ+| π | 3 |
B.(选修4-5不等式选讲)不等式|x-log2x|<x+|log2x|的解集是
C.(选修4-1几何证明选讲)如图所示,AC和AB分别是圆O的切线,且OC=3,AB=4,延长AO到D点,则△ABD的面积是
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分.)
A.(坐标系与参数方程选做题)在极坐标系中,两点 ,
, 间的距离是 .
间的距离是 .
B.(不等式选讲选做题)若不等式 的解集为 .
的解集为 .
C.(几何证明选讲选做题)如图,点 是圆
是圆 上的点,
且
上的点,
且 ,则圆
,则圆 的面积等于 .
的面积等于 .

查看习题详情和答案>>
 (e为参数)化为普通方程是 .
(e为参数)化为普通方程是 .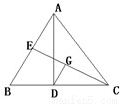
 的距离的最小值是 .
的距离的最小值是 .