题目内容
 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)A.(选修4-4坐标系与参数方程)将参数方程
|
B.(选修4-5 不等式选讲)不等式|x-1|+|2x+3|>5的解集是
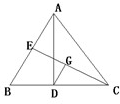
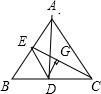
C.(选修4-1 几何证明选讲)如图,在△ABC中,AD是高线,CE是中线,|DC|=|BE|,DG⊥CE于G,且|EC|=8,则|EG|=
分析:A:已知参数方程
可得
两边平方相减即可求解;
B:先将绝对值不等式去掉绝对值写出分段函数,然后分别在每一段上解不等式,最后求它们的并集即可.
C:根据直角三角形的性质可得:|ED|=|BE|,即可得到|ED|=|DC|,结合DG⊥CE于G,可得线段CG垂直并且平分线段CE,进而求出答案.
|
|
B:先将绝对值不等式去掉绝对值写出分段函数,然后分别在每一段上解不等式,最后求它们的并集即可.
C:根据直角三角形的性质可得:|ED|=|BE|,即可得到|ED|=|DC|,结合DG⊥CE于G,可得线段CG垂直并且平分线段CE,进而求出答案.
解答:解:A:∵参数方程
(e为参数),
∴
两边平方得,x2-
=e4+e-4+2-(e4-2+e-4);(x≥2)
∴
-
=1(x≥2).
B:由题意可得:|x-1|+|2x+3|=
所以:当x≥1时,3x+2>5,解得x>1;
当 -
<x<1,x+4>5,解得无解;
当 x≤-
,-3x-2>5,解得x <-
综上所述不等式的解集为 (-∞,-
)∪(1,+∞).
C:因为AD是高线,CE是中线,
所以|ED|=|BE|,
因为|DC|=|BE|,
所以|ED|=|DC|.
又因为DG⊥CE于G,
所以线段CG垂直并且平分线段CE.
因为|EC|=8,
所以|EG|=4.
故答案为
-
=1(x≥2); (-∞,-
)∪(1,+∞);4.
|
∴
|
| y2 |
| 4 |
∴
| x2 |
| 4 |
| y2 |
| 16 |
B:由题意可得:|x-1|+|2x+3|=
|
所以:当x≥1时,3x+2>5,解得x>1;
当 -
| 3 |
| 2 |
当 x≤-
| 3 |
| 2 |
| 7 |
| 3 |
综上所述不等式的解集为 (-∞,-
| 7 |
| 3 |
C:因为AD是高线,CE是中线,
所以|ED|=|BE|,
因为|DC|=|BE|,
所以|ED|=|DC|.
又因为DG⊥CE于G,
所以线段CG垂直并且平分线段CE.
因为|EC|=8,
所以|EG|=4.

故答案为
| x2 |
| 4 |
| y2 |
| 16 |
| 7 |
| 3 |
点评:此题考查参数方程与一般方程的联系和区别与绝对值不等式的解法,并且也考查直角三角形斜边上中线性质,等腰三角形性质等知识点,属于基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分) (2011•渭南三模)选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(2011•渭南三模)选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)