题目内容
A.(选修4-4坐标系与参数方程)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线 的距离的最小值是 .
的距离的最小值是 .B.(选修4-5不等式选讲)不等式|x-log2x|<x+|log2x|的解集是 .
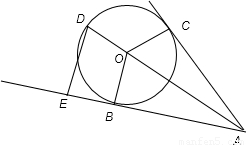
C.(选修4-1几何证明选讲)如图所示,AC和AB分别是圆O的切线,且OC=3,AB=4,延长AO到D点,则△ABD的面积是 .

【答案】分析:A 把曲线的极坐标方程化为普通方程,利用点到直线的距离公式 求出圆心(0,1)到直线的距离,所求的距离
等于此距离减去半径.
B 由不等式可得 x>0,且log2x>0,故有 x>1.
C 由勾股定理可得 AO,由 sinθ= =
=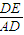 ,可求得高DE,利用S△ABD=
,可求得高DE,利用S△ABD= •AB•DE 求得△ABD的面积.
•AB•DE 求得△ABD的面积.
解答:解:A 曲线ρ=2sinθ 即 x2+y2=2y,x2+(y-1)2=1,表示圆心在(0,1),半径等于1的圆.
直线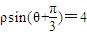 即
即  y+
y+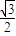 x=4,
x=4,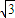 x+y-8=0,
x+y-8=0,
圆心(0,1)到直线的距离等于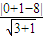 =
= ,点A到直线
,点A到直线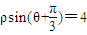 的距离的最小值是
的距离的最小值是  -1=
-1= .
.
B 由对数函数的定义域知,x>0.
当log2x=0时,x=1,经检验,不等式不成立.
当log2x<0时,|x-log2x|=x+|log2x|,不等式不成立.
当log2x>0时,不等式|x-log2x|<x+|log2x|成立,∴x>1.
综上,不等式的解集是 {x|x>1}.
C 如图:作 DE⊥AB,E为垂足,设∠BAO=θ,∵OC=OB=3,AB=AC=4,∴由勾股定理可得 AO=5.
AD=5+3=8,直角三角形BAO中,sinθ=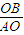 =
=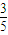 ,直角三角形ADE 中,sinθ=
,直角三角形ADE 中,sinθ=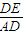 =
=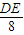 ,
,
∴ =
=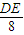 ,∴DE=
,∴DE=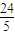 ,S△ABD=
,S△ABD= •AB•DE=
•AB•DE= •4•
•4•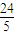 =
=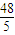 .
.
故答案为:A ;B(1,+∞);C
;B(1,+∞);C 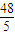 .
.
点评:本题考查把极坐标方程化为普通方程的方法,点到直线的距离公式的应用,绝对值不等式的解法,以及直角三角形中的边角关系.
等于此距离减去半径.
B 由不等式可得 x>0,且log2x>0,故有 x>1.
C 由勾股定理可得 AO,由 sinθ=
 =
= ,可求得高DE,利用S△ABD=
,可求得高DE,利用S△ABD= •AB•DE 求得△ABD的面积.
•AB•DE 求得△ABD的面积.解答:解:A 曲线ρ=2sinθ 即 x2+y2=2y,x2+(y-1)2=1,表示圆心在(0,1),半径等于1的圆.
直线
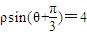 即
即  y+
y+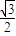 x=4,
x=4,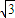 x+y-8=0,
x+y-8=0,圆心(0,1)到直线的距离等于
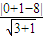 =
= ,点A到直线
,点A到直线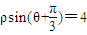 的距离的最小值是
的距离的最小值是  -1=
-1= .
.B 由对数函数的定义域知,x>0.
当log2x=0时,x=1,经检验,不等式不成立.
当log2x<0时,|x-log2x|=x+|log2x|,不等式不成立.
当log2x>0时,不等式|x-log2x|<x+|log2x|成立,∴x>1.
综上,不等式的解集是 {x|x>1}.
C 如图:作 DE⊥AB,E为垂足,设∠BAO=θ,∵OC=OB=3,AB=AC=4,∴由勾股定理可得 AO=5.
AD=5+3=8,直角三角形BAO中,sinθ=
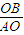 =
=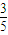 ,直角三角形ADE 中,sinθ=
,直角三角形ADE 中,sinθ=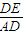 =
=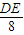 ,
,∴
 =
=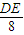 ,∴DE=
,∴DE=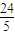 ,S△ABD=
,S△ABD= •AB•DE=
•AB•DE= •4•
•4•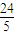 =
=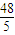 .
.
故答案为:A
 ;B(1,+∞);C
;B(1,+∞);C 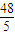 .
.点评:本题考查把极坐标方程化为普通方程的方法,点到直线的距离公式的应用,绝对值不等式的解法,以及直角三角形中的边角关系.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
 (t为参数),C2
(t为参数),C2 (
( 为参数),
为参数), =
= 时,求C1与C2的交点坐标;
时,求C1与C2的交点坐标; (t为参数),C2
(t为参数),C2 (
( 为参数),
为参数), =
= 时,求C1与C2的交点坐标;
时,求C1与C2的交点坐标;