摘要：17．设..A∩. 求A∪B.
网址：http://m.1010jiajiao.com/timu_id_4447838[举报]
设
，（a，b为常数）．当x＞0时，F（x）=f（x），且F（x）为R上的奇函数．
（Ⅰ）若
，且f（x）的最小值为0，求F（x）的表达式；
（Ⅱ）在（Ⅰ）的条件下，
在[2，4]上是单调函数，求k的取值范围．
查看习题详情和答案>>
，（a，b为常数）．当x＞0时，F（x）=f（x），且F（x）为R上的奇函数．（Ⅰ）若
，且f（x）的最小值为0，求F（x）的表达式；（Ⅱ）在（Ⅰ）的条件下，
在[2，4]上是单调函数，求k的取值范围．查看习题详情和答案>>
设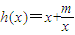
，
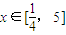，其中m是不等于零的常数，
（1）（理）写出h（4x）的定义域；
（文）m=1时，直接写出h（x）的值域；
（2）（文、理）求h（x）的单调递增区间；
（3）已知函数f（x）（x∈[a，b]），定义：f1（x）=minf（t）|a≤t≤x（x∈[a，b]），f2（x）=maxf（t）|a≤t≤x（x∈[a，b]）．其中，minf（x）|x∈D表示函数f（x）在D上的最小值，maxf（x）|x∈D表示函数f（x）在D上的最大值．例如：f（x）=cosx，x∈[0，π]，则f1（x）=cosx，x∈[0，π]，f2（x）=1，x∈[0，π]．
（理）当m=1时，设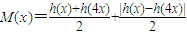
，不等式t≤M1（x）-M2（x）≤n恒成立，求t，n的取值范围；
（文）当m=1时，|h1（x）-h2（x）|≤n恒成立，求n的取值范围．
查看习题详情和答案>>
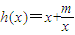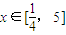，，其中m是不等于零的常数，（1）（理）写出h（4x）的定义域；
（文）m=1时，直接写出h（x）的值域；
（2）（文、理）求h（x）的单调递增区间；
（3）已知函数f（x）（x∈[a，b]），定义：f1（x）=minf（t）|a≤t≤x（x∈[a，b]），f2（x）=maxf（t）|a≤t≤x（x∈[a，b]）．其中，minf（x）|x∈D表示函数f（x）在D上的最小值，maxf（x）|x∈D表示函数f（x）在D上的最大值．例如：f（x）=cosx，x∈[0，π]，则f1（x）=cosx，x∈[0，π]，f2（x）=1，x∈[0，π]．
（理）当m=1时，设
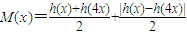，不等式t≤M1（x）-M2（x）≤n恒成立，求t，n的取值范围；（文）当m=1时，|h1（x）-h2（x）|≤n恒成立，求n的取值范围．
查看习题详情和答案>>
，
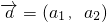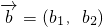，定义一种向量运算：
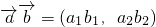，已知
，
，点P（x，y）在函数g（x）=sinx的图象上运动，点Q在函数y=f（x）的图象上运动，且满足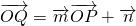
（其中O为坐标原点）．
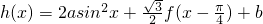，且h（x）的定义域为
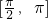，值域为[2，5]，求a，b的值．