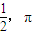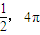题目内容
设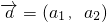 ,
,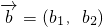 ,定义一种向量运算:
,定义一种向量运算: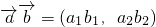 ,已知
,已知 ,
, ,点P(x,y)在函数g(x)=sinx的图象上运动,点Q在函数y=f(x)的图象上运动,且满足
,点P(x,y)在函数g(x)=sinx的图象上运动,点Q在函数y=f(x)的图象上运动,且满足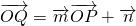 (其中O为坐标原点).
(其中O为坐标原点).
(1)求函数f(x)的解析式;
(2)若函数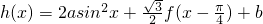 ,且h(x)的定义域为
,且h(x)的定义域为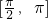 ,值域为[2,5],求a,b的值.
,值域为[2,5],求a,b的值.
解:(1)P(x,y)在函数g(x)=sinx的图象上运动可得,y=sinx,设Q(x1,y1),
∵Q满足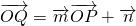 =
=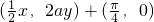 =
=
∴ ?
?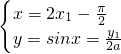
又因为y=sinx
代入可得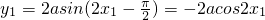
即f(x)=-2acos2x
(2)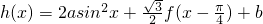
=2asin2x asin2x+b
asin2x+b
=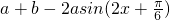
∵x∈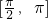 ,2x+
,2x+ ∈[
∈[ π,
π, π]
π]
当a>0时,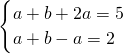
∴a=1,b=2
当a<0时,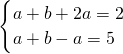
∴a=-1,b=5
分析:(1)设Q(x1,y1),根据定义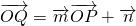 =
=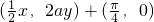 =
= 可得
可得 整理可得
整理可得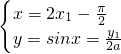 ①把①代入y=sinx可求答案;
①把①代入y=sinx可求答案;
(2)由(1)可得,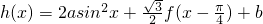 =a+b-(a+
=a+b-(a+ a)cos2x,结合x∈
a)cos2x,结合x∈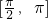 ,可得2x∈[π,2π],结合余弦函数的性质,分a>0,a<0两种情况讨论.
,可得2x∈[π,2π],结合余弦函数的性质,分a>0,a<0两种情况讨论.
点评:本题以新定义为载体,考查了向量的基本运算,二倍角公式的运算,三角函数的性质的应用,属于中档试题,具有一定的综合性.
∵Q满足
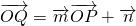 =
=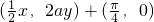 =
=
∴
 ?
?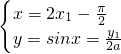
又因为y=sinx
代入可得
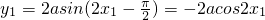
即f(x)=-2acos2x
(2)
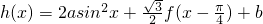
=2asin2x
 asin2x+b
asin2x+b=
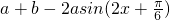
∵x∈
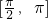 ,2x+
,2x+ ∈[
∈[ π,
π, π]
π]当a>0时,
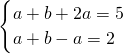
∴a=1,b=2
当a<0时,
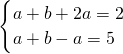
∴a=-1,b=5
分析:(1)设Q(x1,y1),根据定义
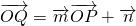 =
=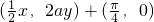 =
= 可得
可得 整理可得
整理可得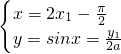 ①把①代入y=sinx可求答案;
①把①代入y=sinx可求答案;(2)由(1)可得,
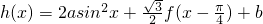 =a+b-(a+
=a+b-(a+ a)cos2x,结合x∈
a)cos2x,结合x∈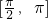 ,可得2x∈[π,2π],结合余弦函数的性质,分a>0,a<0两种情况讨论.
,可得2x∈[π,2π],结合余弦函数的性质,分a>0,a<0两种情况讨论.点评:本题以新定义为载体,考查了向量的基本运算,二倍角公式的运算,三角函数的性质的应用,属于中档试题,具有一定的综合性.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
设向量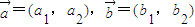 ,定义一种向量积:
,定义一种向量积: .已知
.已知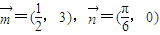 ,点P在y=sinx的图象上运动,点Q在y=f(x)的图象上运动,且满足
,点P在y=sinx的图象上运动,点Q在y=f(x)的图象上运动,且满足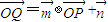 (其中O为坐标原点),则y=f(x)的最大值及最小正周期分别是( )
(其中O为坐标原点),则y=f(x)的最大值及最小正周期分别是( )
A.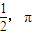
B.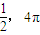
C.3,π
D.3,4π
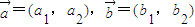 ,定义一种向量积:
,定义一种向量积: .已知
.已知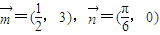 ,点P在y=sinx的图象上运动,点Q在y=f(x)的图象上运动,且满足
,点P在y=sinx的图象上运动,点Q在y=f(x)的图象上运动,且满足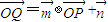 (其中O为坐标原点),则y=f(x)的最大值及最小正周期分别是( )
(其中O为坐标原点),则y=f(x)的最大值及最小正周期分别是( )A.
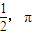
B.
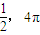
C.3,π
D.3,4π
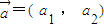 ,
,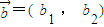 ,定义一种向量运算:
,定义一种向量运算: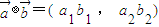 ,已知
,已知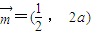 ,
,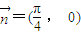 ,点P(x,y)在函数g(x)=sinx的图象上运动,点Q在函数y=f(x)的图象上运动,且满足
,点P(x,y)在函数g(x)=sinx的图象上运动,点Q在函数y=f(x)的图象上运动,且满足 (其中O为坐标原点).
(其中O为坐标原点).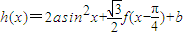 ,且h(x)的定义域为
,且h(x)的定义域为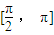 ,值域为[2,5],求a,b的值.
,值域为[2,5],求a,b的值.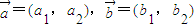 ,定义一种向量积:
,定义一种向量积: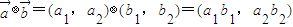 .已知
.已知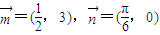 ,点P在y=sinx的图象上运动,点Q在y=f(x)的图象上运动,且满足
,点P在y=sinx的图象上运动,点Q在y=f(x)的图象上运动,且满足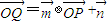 (其中O为坐标原点),则y=f(x)的最大值及最小正周期分别是( )
(其中O为坐标原点),则y=f(x)的最大值及最小正周期分别是( )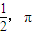
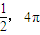
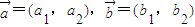 ,定义一种向量积:
,定义一种向量积: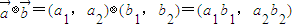 .已知
.已知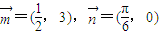 ,点P在y=sinx的图象上运动,点Q在y=f(x)的图象上运动,且满足
,点P在y=sinx的图象上运动,点Q在y=f(x)的图象上运动,且满足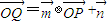 (其中O为坐标原点),则y=f(x)的最大值及最小正周期分别是( )
(其中O为坐标原点),则y=f(x)的最大值及最小正周期分别是( )