题目内容
设 ,(a,b为常数).当x>0时,F(x)=f(x),且F(x)为R上的奇函数.
,(a,b为常数).当x>0时,F(x)=f(x),且F(x)为R上的奇函数.(Ⅰ)若
 ,且f(x)的最小值为0,求F(x)的表达式;
,且f(x)的最小值为0,求F(x)的表达式;(Ⅱ)在(Ⅰ)的条件下,
 在[2,4]上是单调函数,求k的取值范围.
在[2,4]上是单调函数,求k的取值范围.
【答案】分析:(1)根据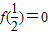 可消去b,再由f(x)的最小值为0确定f(x)的解析式,最后求出F(x)的解析式.
可消去b,再由f(x)的最小值为0确定f(x)的解析式,最后求出F(x)的解析式.
(2)根据(1)先将g(x)的解析式化简为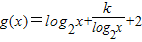 ,再将t=log2x代入进行换元,可得答案.
,再将t=log2x代入进行换元,可得答案.
解答:解:(1)f(x)=alog22x+blog2x+1
由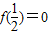 得a-b+1=0,
得a-b+1=0,
∴f(x)=alog22x+(a+1)log2x+1
若a=0则f(x)=log2x+1无最小值.
∴a≠0.
欲使f(x)取最小值为0,只能使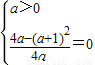 ,知a=1,b=2.
,知a=1,b=2.
∴f(x)=log22x+2log2x+
设x<0则-x>0,
∴F(x)=f(-x)=log22(-x)+2log2(-x)+1
又F(-x)=-F(x),
∴F(x)=-log22(-x)-2log2(-x)-1
又F(0)=0∴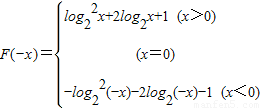
(2)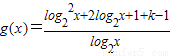 =
=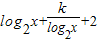 .x∈[2,4].
.x∈[2,4].
得log2x=t.则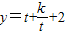 ,t∈[1,2].
,t∈[1,2].
∴当k≤0,或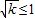 或
或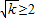 时,y为单调函数.
时,y为单调函数.
综上,k≤1或k≥4.
点评:主要考查求函数解析式的问题.本题属于较难类型的题.
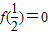 可消去b,再由f(x)的最小值为0确定f(x)的解析式,最后求出F(x)的解析式.
可消去b,再由f(x)的最小值为0确定f(x)的解析式,最后求出F(x)的解析式.(2)根据(1)先将g(x)的解析式化简为
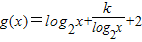 ,再将t=log2x代入进行换元,可得答案.
,再将t=log2x代入进行换元,可得答案.解答:解:(1)f(x)=alog22x+blog2x+1
由
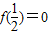 得a-b+1=0,
得a-b+1=0,∴f(x)=alog22x+(a+1)log2x+1
若a=0则f(x)=log2x+1无最小值.
∴a≠0.
欲使f(x)取最小值为0,只能使
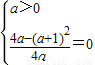 ,知a=1,b=2.
,知a=1,b=2.∴f(x)=log22x+2log2x+
设x<0则-x>0,
∴F(x)=f(-x)=log22(-x)+2log2(-x)+1
又F(-x)=-F(x),
∴F(x)=-log22(-x)-2log2(-x)-1
又F(0)=0∴
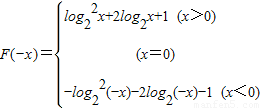
(2)
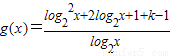 =
=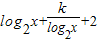 .x∈[2,4].
.x∈[2,4].得log2x=t.则
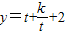 ,t∈[1,2].
,t∈[1,2].∴当k≤0,或
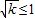 或
或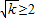 时,y为单调函数.
时,y为单调函数.综上,k≤1或k≥4.
点评:主要考查求函数解析式的问题.本题属于较难类型的题.

练习册系列答案
相关题目
 (a,b为常数),且方程
(a,b为常数),且方程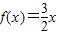 有两个实根为x1=-1,x2=2,
有两个实根为x1=-1,x2=2, (a,b为常数),且方程
(a,b为常数),且方程 有两个实根为x1=-1,x2=2,
有两个实根为x1=-1,x2=2, (a,b为常数),且方程
(a,b为常数),且方程 有两个实根为x1=-1,x2=2,
有两个实根为x1=-1,x2=2, (a,b为常数),且方程
(a,b为常数),且方程 有两个实根为x1=-1,x2=2,
有两个实根为x1=-1,x2=2,