为了比较“传统式教学法”与我校所创立的“三步式教学法”的教学效果．共选100名学生随机分成两个班，每班50名学生，其中一班采取“传统式教学法”，二班实行“三步式教学法”
（Ⅰ）若全校共有学生2000名，其中男生1100名，现抽取100名学生对两种教学方式的受欢迎程度进行问卷调查，应抽取多少名女生？
（Ⅱ）下表1，2分别为实行“传统式教学”与“三步式教学”后的数学成绩：
表1

数学成绩	90分以下	90-120分	120-140分	140分以上
频    数	15	20	10	5

表2

数学成绩	90分以下	90-120分	120-140分	140分以上
频    数	5	40	3	2

完成下面2×2列联表，并回答是否有99%的把握认为这两种教学法有差异．

班  次	120分以下（人数）	120分以上（人数）	合计（人数）
一班
二班
合计

参考数据：

P（K2≥k0）	0.40	0.25	0.10	0.05	0.010	0.005
k0	0.708	1.323	2.706	3.841	6.635	7.879

（2009•宁波模拟）某市十所重点中学进行高三联考，共有5000名考生，为了了解数学学科的学习情况，现从中随机抽出若干名学生在这次测试中的数学成绩，制成如图所示的频率分布直方图．据此估计全体考生中120分及以上的学生数为．

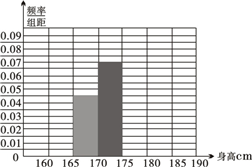（2012•江西模拟）某省重点中学从高二年级学生中随机地抽取120名学生，测得身高情况如下表所示．
（1）请在频率分布表中的①，②位置上填上适当的数据，并补全频率分布直方图；

分组	频数	频率
[160，165）	6	0.05
[165，170）	27	0.225
[170，175）	42	②
[175，180）	36	0.3
[180，185）	①	0.05
[185，180）	3	0.0258
合计	120	1

（2）现从180cm～190cm这些同学中随机地抽取两名，求身高为185cm以上（包括185cm）的同学被抽到的概率．

杨辉是中国南宋末年的一位杰出的数学家、数学教育家，他的数学研究与教育工作的重点是在计算技术方面，杨辉三角是杨辉的一大重要研究成果，它的许多性质与组合数的性质有关．图是一个7阶的杨辉三角．
给出下列五个命题：
①记第i（i∈N^*）行中从左到右的第j（j∈N^*）个数为a_ij，则数列{a_ij}的通项公式为C_i^j；
②第k行各数的和是2^k；
③n阶杨辉三角中共有

(n+1)2

2

个数；
④n阶杨辉三角的所有数的和是2ⁿ⁺¹-1．
其中正确命题的序号为．

（2012•郑州二模）为加强中学生实践、创新能力和同队精神的培养，促进教育教学改革，郑州市教育局举办了全市中学生创新知识竞赛．某校举行选拔赛，共有200名学生参加，为了解成绩情况，从中抽取50名学生的成绩（得分均为整数，满分为100分）进行统计．请你根据尚未完成的频率分布表，解答下列问题：

分组		频数	频率
一	60.5～70.5	A	0.26
二	70.5～80.5	15	C
三	80.5～90.5	18	0.36
四	90.5～100.5	B	D
合计		50	E

（I ）若用系统抽样的方法抽取50个样本，现将所有学生随机地编号为000，001，002，…，199，试写出第二组第一位学生的编号；
（II）求出a，b，c，d，e的值（直接写出结果），并作出频率分布直方图；
（III）若成绩在95.5分以上的学生为一等奖，现在，从所有一等奖同学中随机抽取5名同学代表学校参加决赛，某班共有3名同学荣获一等奖，若该班同学参加决赛人数记为X，求X的分布列和数学期望．