Question

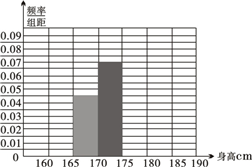（2012•江西模拟）某省重点中学从高二年级学生中随机地抽取120名学生，测得身高情况如下表所示．
（1）请在频率分布表中的①，②位置上填上适当的数据，并补全频率分布直方图；

分组	频数	频率
[160，165）	6	0.05
[165，170）	27	0.225
[170，175）	42	②
[175，180）	36	0.3
[180，185）	①	0.05
[185，180）	3	0.0258
合计	120	1

（2）现从180cm～190cm这些同学中随机地抽取两名，求身高为185cm以上（包括185cm）的同学被抽到的概率．

Answer 1

分析：（1）根据题意，设表中的①的数据为m，②的数据为n，根据频率、频数的关系可得m=120×0.05=6，n=

42

120

=0.35，据此可以做出频率分步直方图；
（2）记身高在180～185的人编号a，b，c，d，e，f；身高在185～190的人编号1，2，3；由列举法可得从9人中抽取2人的所有可能情况，分析可得身高为185cm以上（包括185cm）的同学被抽到的情况数目，由等可能事件的概率公式，计算可得答案．

解答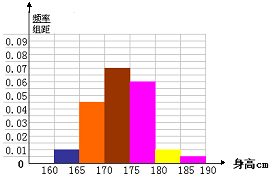：解：（1）设表中的①的数据为m，②的数据为n，
则m=120×0.05=6，n=

42

120

=0.35，
则表中的①的数据为6，②的数据为0.35．
作图
（2）记身高在180～185的人编号a，b，c，d，e，f；
身高在185～190的人编号1，2，3；
从9人中抽取2人的所有可能情况为：（a，b），（a，c），（a，d），（a，e），（a，f），（a，1），（a，2），（a，3）（b，c），（b，d），（b，e），（b，f），（b，1），（b，2），（b，3）（c，d），（c，e），（c，f），（c，1），（c，2），（c，3）（d，e），（d，f），（d，1），（d，2），（d，3）（e，f），（e，1），（e，2），（e，3）（f，1），（f，2），（f，3）（1，2），（1，3）（2，3）
其中身高为185cm以上（包括185cm）的同学被抽到的情况有21种，
故其概率为P=

21

36

=

7

12

．

点评：本题考查频率分布表的运用与频率分步直方图的作法，关键是根据频率、频数的关系，将表中数据补充完整．