摘要：12．设同时满足条件①≤bn+1(n∈N?),②bn≤M(n∈N?.M是与n无关的常数)的无穷数列{bn}叫“特界 数列． (1)若数列{an}是等差数列.Sn是其前n项和.a3＝4. S3＝18.求Sn, 中的数列{Sn}是否为“特界 数列.并说明理由． [解析] (1)设等差数列{an}的公差为d.则 a1+2d＝4,3a1+3d＝18 解得a1＝8.d＝-2 ∴Sn＝na1+d＝-n2+9n (2)∵-Sn+1＝ ＝＝＝-1＜0 ∴＜Sn+1.∴数列{Sn}适合条件① 又Sn＝-n2+9n＝-2+(n∈N?) ∴当n＝4或5时.Sn取最大值20 即Sn≤20.∴{Sn}适合条件② 综上.数列{Sn}是“特界 数列．
网址：http://m.1010jiajiao.com/timu_id_4436111[举报]
设同时满足条件：①
≤bn＋1(n∈N＋)；②bn≤M(n∈N＋，M是与n无关的常数)的无穷数列{bn}叫“特界”数列.
(1)若数列{an}为等差数列，Sn是其前n项和，a3＝4，S3＝18，求Sn；
(2)判断(1)中的数列{Sn}是否为“特界”数列，并说明理由.
查看习题详情和答案>>
设同时满足条件：①
≤bn+1（n∈N*）；②bn≤M（n∈N*，M是与n无关的常数）的无穷数列{bn} 叫“特界”数列．
（Ⅰ）若数列{an} 为等差数列，Sn是其前n项和，a3=4，S3=18，求Sn；
（Ⅱ）判断（Ⅰ）中的数列{Sn}是否为“特界”数列，并说明理由． 查看习题详情和答案>>
| bn+bn+2 | 2 |
（Ⅰ）若数列{an} 为等差数列，Sn是其前n项和，a3=4，S3=18，求Sn；
（Ⅱ）判断（Ⅰ）中的数列{Sn}是否为“特界”数列，并说明理由． 查看习题详情和答案>>
设同时满足条件：①
≤bn+1（n∈N*）；②bn≤M（n∈N*，M是与n无关的常数）的无穷数列{bn} 叫“特界”数列．
（Ⅰ）若数列{an} 为等差数列，Sn是其前n项和，a3=4，S3=18，求Sn；
（Ⅱ）判断（Ⅰ）中的数列{Sn}是否为“特界”数列，并说明理由．
查看习题详情和答案>>
| bn+bn+2 |
| 2 |
（Ⅰ）若数列{an} 为等差数列，Sn是其前n项和，a3=4，S3=18，求Sn；
（Ⅱ）判断（Ⅰ）中的数列{Sn}是否为“特界”数列，并说明理由．
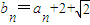，问数列{bn}中是否存在不同的3项，使之成为等比数列？若存在，试写出任意符合条件的3项；若不存在，请说明理由．