摘要： 解:通过观察凸四边形和五边形对角线的条数.可得到凸八边形的对角线条数应该是20条.思考过程:凸n边形每个顶点不能和它自己以及它的两个邻点作对角线.所以可做的对角线条数是(n-3), 凸n边形有n个顶点.所以可做n(n-3)条.由于对角线AB和BA是同一条.所以凸n边形共有条对角线.当n=8时.有条对角线.
网址：http://m.1010jiajiao.com/timu_id_4435308[举报]
如图，一次函数y=kx+b（k不为0）的图象与x轴和y轴交于A、B两点
（1）求这个一次函数的解析式．
（2）通过观察图象，写出不等式kx+b＜0的解集是什么？
（3）在x轴的正半轴上是否存在点P，使△AOB和△POB相似？若存在，求出点P坐标；若不存在，说明理由．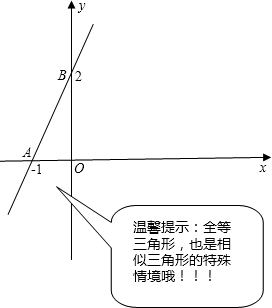
查看习题详情和答案>>
（1）求这个一次函数的解析式．
（2）通过观察图象，写出不等式kx+b＜0的解集是什么？
（3）在x轴的正半轴上是否存在点P，使△AOB和△POB相似？若存在，求出点P坐标；若不存在，说明理由．
查看习题详情和答案>>
先阅读下面的材料，然后解答问题：通过观察，发现方程：
x+
=2+
的解为x1=2，x2=
；
x+
=3+
的解为x1=3，x2=
；
x+
=4+
的解为x1=4，x2=
；…
（1）观察上述方程的解，猜想关于x的方程x+
=5+
的解是 ；
（2）根据上面的规律，猜想关于x的方程x+
=c+
的解是 ；
（3）把关于x的方程
=a+
变形为方程x+
=c+
的形式是 ，方程的解是 ．
查看习题详情和答案>>
x+
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
x+
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| 3 |
x+
| 1 |
| x |
| 1 |
| 4 |
| 1 |
| 4 |
（1）观察上述方程的解，猜想关于x的方程x+
| 1 |
| x |
| 1 |
| 5 |
（2）根据上面的规律，猜想关于x的方程x+
| 1 |
| x |
| 1 |
| c |
（3）把关于x的方程
| x2-x+1 |
| x-1 |
| 1 |
| a-1 |
| 1 |
| x |
| 1 |
| c |
例：解方程组
解：由①+②得：4000x+4000y=16000
即x+y=4 ③
由①-②得2x-2y=2
即x-y=1 ④
[归纳]：对于大系数的二元一次方程组，当用代入法和加减法解非常麻烦，可以通过观察各项系数的特点，寻求特殊解法：
结合例子：模仿解下列方程组
．
查看习题详情和答案>>
|
解：由①+②得：4000x+4000y=16000
即x+y=4 ③
由①-②得2x-2y=2
即x-y=1 ④
[归纳]：对于大系数的二元一次方程组，当用代入法和加减法解非常麻烦，可以通过观察各项系数的特点，寻求特殊解法：
结合例子：模仿解下列方程组
|
通过观察发现方程x+
=2+
的解是x1=2或x2=
；x+
=3+
的解是x1=3或x2=
；按照你发现的规律，则方程x+
=b+
的解是（ ）
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| x+1 |
| 1 |
| b+1 |
A、x1=b或x2=
| ||
B、x1=b或x2=
| ||
C、x1=b+1或x2=
| ||
D、x1=b或x2=-
|