摘要:例1设无穷等差数列的前n项和为. (1)若首项.公差.求满足的正整数k, (2)求所有的无穷等差数列.使得对于一切正整数k都有成立. 例2 如图.64个正数排成8行8列方阵.符号表示位于第i行第j列的正数.已知每一行的数成等差数列.每一列的数成等比数列.且各列数的公比都等于.若... (1)求的通项公式, (2)记第行各项和为.求的值及数列 的通项公式, (3)若.求的值. 例3 函数对任意都有 (1)求和的值. (2)数列满足:=.数列是等差数列吗? (3)令.试比较与的大小. 例4. 已知数列{an}满足a1=a, an+1=1+我们知道当a取不同的值时.得到不同的数列.如当a=1时.得到无穷数列: (Ⅰ)求当a为何值时a4=0, (Ⅱ)设数列{bn}满足b1=-1, bn+1=.求证a取数列{bn}中的任一个数.都可以得到一个有穷数列{an}, (Ⅲ)若.求a的取值范围.
网址:http://m.1010jiajiao.com/timu_id_4429841[举报]
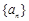 的前n项和为
的前n项和为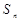 .
.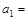 ,公差
,公差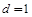 ,满足
,满足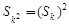 的正整数k=
;
的正整数k=
; 的前n项和为
的前n项和为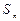 .
. ,公差
,公差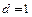 ,满足
,满足 的正整数k= ;
的正整数k= ;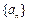 的前n项和为
的前n项和为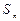 .
.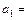 ,公差
,公差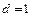 ,满足
,满足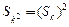 的正整数k= ;
的正整数k= ;