摘要: 数列满足.(1)求证:数列是等比数列, (2)求数列的通项公式,(3)求数列的前n项和.
网址:http://m.1010jiajiao.com/timu_id_4429788[举报]
等比数列{cn}满足cn+1+cn=5•22n-1,n∈N*,数列{an}满足an=log2cn
(Ⅰ)求{an}的通项公式;
(Ⅱ)数列{bn}满足bn=
,Tn为数列{bn}的前n项和.求证:Tn<
;
(Ⅲ)是否存在正整数m,n(1<m<n),使得T1,Tm,Tn成等比数列?若存在,求出所有m,n 的值;若不存在,请说明理由.
查看习题详情和答案>>
(Ⅰ)求{an}的通项公式;
(Ⅱ)数列{bn}满足bn=
| 1 |
| an•an+1 |
| 1 |
| 2 |
(Ⅲ)是否存在正整数m,n(1<m<n),使得T1,Tm,Tn成等比数列?若存在,求出所有m,n 的值;若不存在,请说明理由.
等比数列{an}同时满足下列三个条件:①a1+a6=33;②a3a4=32;③三个数4a2,2a3,a4依次成等差数列.
(Ⅰ)试求数列{an}的通项公式;
(Ⅱ)记bn=![]() ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn;
(Ⅲ)设Sn是数列{an}的前n项和,证明![]() .
.
等比数列{an}中,a1,a2,a3分别是下表第一、二、三行中的某一个数,且a1,a2,a3中的任何两个数不在下表的同一列.

(1)试确定a1,a2,a3的值,并求数列{an}的通项公式.
(2)若数列{bn}满足bn=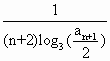 ,记数列{bn}的前n项和为Sn,证明:Sn<
,记数列{bn}的前n项和为Sn,证明:Sn<![]() .
.
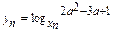 满足
满足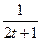 ,yt=
,yt=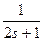 (s,t∈N,且s≠t)共中a为常数,且1<a<
(s,t∈N,且s≠t)共中a为常数,且1<a<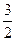 ,试判断,是否存在自然
,试判断,是否存在自然