摘要:(一)数列 数列. 等差数列及其通项公式.等差数列前n项和公式. 等比数列及其通项公式.等比数列前n项和公式. (二)极限 教学归纳法.数学归纳法应用. 数列的极限. 函数的极限.根限的四则运算.函数的连续性. (三)导数 导数的概念.导数的几何意义.几种常见函数的导数. 两个函数的和.差.积.商和导数.复习函数的导数.基本导数公式. 利用导数研究函数的单调性和极值.函数的最大值和最小值.
网址:http://m.1010jiajiao.com/timu_id_4429663[举报]
已知等差数列{an}的前n项的和记为Sn.如果a4=-12,a8=-4.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求Sn的最小值及其相应的n的值;
(Ⅲ)从数列{an}中依次取出a1,a2,a4,a8,…,a2n-1,…,构成一个新的数列{bn},求{bn}的前n项和.
查看习题详情和答案>>
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求Sn的最小值及其相应的n的值;
(Ⅲ)从数列{an}中依次取出a1,a2,a4,a8,…,a2n-1,…,构成一个新的数列{bn},求{bn}的前n项和.
已知等差数列{an}的前n项的和记为Sn.如果a4=-12,a8=-4.
(1)求数列{an}的通项公式;(2)求Sn的最小值及其相应的n的值;
(3)从数列{an}中依次取出a1,a2,a4,a8,…, ,…,构成一个新的数列{bn},
,…,构成一个新的数列{bn},
求{bn}的前n项和
查看习题详情和答案>>
已知等差数列{an}的前n项的和记为Sn.如果a4=-12, a8=-4.
(1)求数列{an}的通项公式;
(2)求Sn的最小值及其相应的n的值;
(3)从数列{an}中依次取出a1,a2,a4,a8,…, ,…,构成一个新的数列{bn},求{bn}的前n项和.
,…,构成一个新的数列{bn},求{bn}的前n项和.
查看习题详情和答案>>
 ,…,构成一个新的数列{bn},
,…,构成一个新的数列{bn},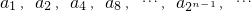 ,构成一个新的数列{bn},求{bn}的前n项和.
,构成一个新的数列{bn},求{bn}的前n项和.