摘要： 设f(x)是定义在[0, 1]上的函数.若存在x*∈(0.1).使得f(x)在[0, x*]上单调递增.在[x*.1]上单调递减.则称f(x)为[0, 1]上的单峰函数.x*为峰点.包含峰点的区间为含峰区间．对任意的[0.l]上的单峰函数f(x).下面研究缩短其含峰区间长度的方法． (I)证明:对任意的x1.x2∈(0.1).x1＜x2.若f(x1)≥f(x2).则(0.x2)为含峰区间,若f(x1)≤f(x2).则(x*.1)为含峰区间, (II)对给定的r.证明:存在x1.x2∈(0.1).满足x2-x1≥2r.使得由(I)所确定的含峰区间的长度不大于 0.5+r, (III)选取x1.x2∈.x1＜x2.由(I)可确定含峰区间为(0.x2)或(x1.1).在所得的含峰区间内选取x3.由x3与x1或x3与x2类似地可确定一个新的含峰区间．在第一次确定的含峰区间为(0.x2)的情况下.试确定x1.x2.x3的值.满足两两之差的绝对值不小于0.02.且使得新的含峰区间的长度缩短到0.34.(区间长度等于区间的右端点与左端点之差)
网址：http://m.1010jiajiao.com/timu_id_4429650[举报]
的函数，若f(x)＝
则
等于
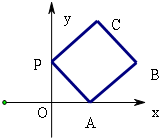（北京卷理14）如图放置的边长为1的正方形PABC沿x轴滚动．设顶点p（x，y）的轨迹方程是y=f（x），则f（x）的最小正周期为说明：“正方形PABC沿X轴滚动”包括沿x轴正方向和沿x轴负方向滚动．沿x轴正方向滚动指的是先以顶点A为中心顺时针旋转，当顶点B落在x轴上时，再以顶点B为中心顺时针旋转，如此继续．类似地，正方形PABC可以沿x轴负方向滚动． 查看习题详情和答案>>
（04年北京卷文）(14分)
函数f(x)定义在[0,1]上,满足
且f(1)=1,在每个区间
=1,2,…)上, y=f(x) 的图象都是平行于x轴的直线的一部分.
(Ⅰ)求f(0)及
的值,并归纳出
)的表达式;
(Ⅱ)设直线
轴及y=f(x)的图象围成的矩形的面积为
, 求a1,a2及
的值.
（05年北京卷理）（14分）
设
是定义在[0，1]上的函数，若存在
，使得在[0，
]上单调递增，在[，1]单调递减，则称为[0，1]上的单峰函数，为峰点，包含峰点的区间为含峰区间
对任意的[0，1]上的单峰函数，下面研究缩短其含峰区间长度的方法
（Ⅰ）证明：对任意的
, 
,若
，则（0，
）为含峰区间；若
，则（
，1）为含峰区间；
（Ⅱ）对给定的
（0<<0.5），证明：存在,满足
，使得由（Ⅰ）确定的含峰区间的长度不大于0.5+;
(Ⅲ)选取, 由（Ⅰ）可确定含峰区间为（0，）或（，1），在所得的含峰区间内选取
,由与或与类似地可确定是一个新的含峰区间．在第一次确定的含峰区间为（0，）的情况下，试确定
的值，满足两两之差的绝对值不小于0.02且使得新的含峰区间的长度缩短到0.34
（区间长度等于区间的右端点与左端点之差）