题目内容
(05北京卷)已知函数f(x)=-x3+3x2+9x+a,
(I)求f(x)的单调递减区间;
(II)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
【答案】
(1)单调递减区间为(-∞,-1),(3,+∞);(2)7.
【解析】
试题分析:分析:(I):求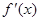 ,解不等式
,解不等式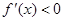 即可.
即可.
(II):求出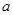 ,进而求出最小值.
,进而求出最小值.
解:(I) f ’(x)=-3x2+6x+9.令f ‘(x)<0,解得x<-1或x>3,
所以函数f(x)的单调递减区间为(-∞,-1),(3,+∞).
(II)因为f(-2)=8+12-18+a=2+a,f(2)=-8+12+18+a=22+a,
所以f(2)>f(-2).因为在(-1,3)上f ‘(x)>0,所以f(x)在[-1, 2]上单调递增,又由于f(x)在[-2,-1]上单调递减,因此f(2)和f(-1)分别是f(x)在区间[-2,2]上的最大值和最小值,于是有 22+a=20,解得 a=-2.
故f(x)=-x3+3x2+9x-2,因此f(-1)=1+3-9-2=-7,
即函数f(x)在区间[-2,2]上的最小值为-7.
考点:本题主要考查多项式函数的导数公式及运用导数求单调区间和函数最值。
点评:应注意先比较f(2)f(-2)的大小,然后判定哪个是最大值而求解.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
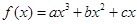 在点
在点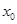 处取得极大值
处取得极大值 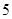 ,其导函数
,其导函数 的图象经过点
的图象经过点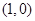 ,
,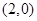 ,如图所示.求:
,如图所示.求:
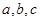 的值.
的值.