摘要：(1)函数的递增区间为 , (2)函数的递减区间为 变题:已知在[0, 1]上是减函数.则实数的取值范围是＿＿＿＿.
网址：http://m.1010jiajiao.com/timu_id_4429504[举报]
函数
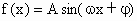的图象如图所示，试依图推出：
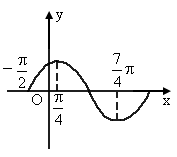
(1)f(x)
的最小正周期；(2)f(x)=0
时x的取值集合；(3)
使f(x)＜0的x的取值集合；(4)f(x)
的单调递增区间和递减区间；(5)
使f(x)取最小值的x的取值集合；(6)
图象的对称轴方程；(7)
图象的对称中心；(8)
要使f(x)成为偶函数，就对f(x)的图象作怎样的平移变换． 查看习题详情和答案>>函数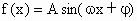
的图象如图所示，试依图推出：
(1)f(x)的最小正周期；
(2)f(x)=0时x的取值集合；
(3)使f(x)＜0的x的取值集合；
(4)f(x)的单调递增区间和递减区间；
(5)使f(x)取最小值的x的取值集合；
(6)图象的对称轴方程；
(7)图象的对称中心；
(8)要使f(x)成为偶函数，就对f(x)的图象作怎样的平移变换．
查看习题详情和答案>>探究函数
的最小值，并确定取得最小值时x的值.列表如下：
x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 4.8 | 7.57 | … |
请观察表中y值随x值变化的特点，完成以下的问题.
函数
在区间（0，2）上递减；
函数在区间 上递增.
当
时，
.
证明：函数
在区间（0，2）递减.
思考:
函数
时，有最值吗？是最大值还是最小值？此时x为何值？（直接回答结果，不需证明）
查看习题详情和答案>>
满足：
，且在区间
与
上分别递减和递增，则不等式
的解集为（ ）
；B．
；D．
探究函数
的最小值，并确定取得最小值时x的值．列表如下，请观察表中y值随x值变化的特点，完成以下的问题．
已知：函数
在区间（0，2）上递减，问：
（1）函数
在区间______上递增．当x=______时，y最小=______．
（2）证明：函数
在区间（0，2）递减；
（3）思考：函数
有最大值或最小值吗？如有，是多少？此时x为何值？（直接回答结果，不需证明）
查看习题详情和答案>>
的最小值，并确定取得最小值时x的值．列表如下，请观察表中y值随x值变化的特点，完成以下的问题．| x | … | 0.5 | 1 | 1.5 | 1.7 | 2 | 2.1 | 2.3 | 3 | 4 | 7 | … |
| y | … | 64.25 | 17 | 9.36 | 8.43 | 8 | 8.04 | 8.31 | 10.7 | 17 | 49.33 | … |
在区间（0，2）上递减，问：（1）函数
在区间______上递增．当x=______时，y最小=______．（2）证明：函数
在区间（0，2）递减；（3）思考：函数
有最大值或最小值吗？如有，是多少？此时x为何值？（直接回答结果，不需证明）查看习题详情和答案>>