题目内容
函数
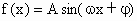 的图象如图所示,试依图推出:
的图象如图所示,试依图推出:
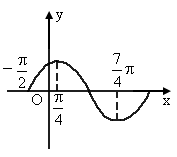
(1)f(x)
的最小正周期;(2)f(x)=0
时x的取值集合;(3)
使f(x)<0的x的取值集合;(4)f(x)
的单调递增区间和递减区间;(5)
使f(x)取最小值的x的取值集合;(6)
图象的对称轴方程;(7)
图象的对称中心;(8)
要使f(x)成为偶函数,就对f(x)的图象作怎样的平移变换.
答案:略
解析:
解析:
|
解:由图象知: (1)最小正周期是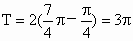 . .
(2) 在一个周期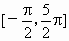 中使f(x)=0的x是 中使f(x)=0的x是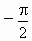 ,p
, ,p
,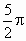 , ,
故所求的 x的取值集合是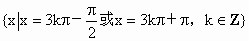 . .
(3) 使f(x)<0的x的集合是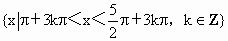 . .
(4)f(x) 的增区间是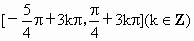 . .
减区间是 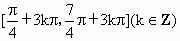 . .
(5)f(x) 取最小值时x的集合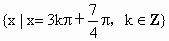 . .
(6) 对称轴方程是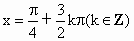 . .
(7) 对称中心是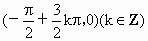 . .
(8) 要使f(x)成为偶函数可以把图象向左平移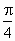 个单位.(不唯一) 个单位.(不唯一) |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
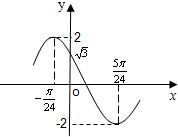 已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π),且函数的图象如图所示,则点(ω,φ)的坐标是( )
已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π),且函数的图象如图所示,则点(ω,φ)的坐标是( )A、(2,
| ||
B、(4,
| ||
C、(2,
| ||
D、(4,
|
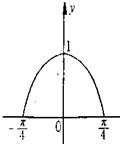 已知函y=f(x)定义在[-
已知函y=f(x)定义在[-| π |
| 4 |
| π |
| 4 |
| A、y=sinx |
| B、y=-sinx•cosx |
| C、y=sinx•cosx |
| D、y=cosx |
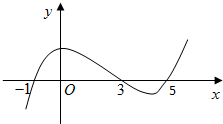 函数y=f(x)导函数的图象如图所示,则下列说法正确的是:( )
函数y=f(x)导函数的图象如图所示,则下列说法正确的是:( )
