摘要：组合数公式:,,
网址：http://m.1010jiajiao.com/timu_id_4428768[举报]
对于数列{An}：A1，A2，A3，…，An，若不改变A1，仅改变A2，A3，…，An中部分项的符号，得到的新数列{an}称为数列{An}的一个生成数列．如仅改变数列1，2，3，4，5的第二、三项的符号可以得到一个生成数列1，-2，-3，4，5．已知数列{an}为数列{
}(n∈N*)的生成数列，Sn为数列{an}的前n项和．
（1）写出S3的所有可能值；
（2）若生成数列{an}满足：S3n=
(1-
)，求{an}的通项公式；
（3）证明：对于给定的n∈N*，Sn的所有可能值组成的集合为：{x|x=
，m∈N*，m≤2n-1}．
查看习题详情和答案>>
| 1 |
| 2n |
（1）写出S3的所有可能值；
（2）若生成数列{an}满足：S3n=
| 1 |
| 7 |
| 1 |
| 8n |
（3）证明：对于给定的n∈N*，Sn的所有可能值组成的集合为：{x|x=
| 2m-1 |
| 2n |
对于数列{An}：A1，A2，A3，…，An，若不改变A1，仅改变A2，A3，…，An中部分项的符号，得到的新数列{an}称为数列{An}的一个生成数列．如仅改变数列1，2，3，4，5的第二、三项的符号可以得到一个生成数列1，-2，-3，4，5．已知数列{an}为数列{
}(n∈N*)的生成数列，Sn为数列{an}的前n项和．
（1）写出S3的所有可能值；
（2）若生成数列{an}的通项公式为an=
，k∈N，求Sn；
（3）用数学归纳法证明：对于给定的n∈N*，Sn的所有可能值组成的集合为：{x|x=
，m∈N*，m≤2n-1}．
查看习题详情和答案>>
| 1 |
| 2n |
（1）写出S3的所有可能值；
（2）若生成数列{an}的通项公式为an=
|
（3）用数学归纳法证明：对于给定的n∈N*，Sn的所有可能值组成的集合为：{x|x=
| 2m-1 |
| 2n |
对于数列{An}：A1，A2，A3，…，An，若不改变A1，仅改变A2，A3，…，An中部分项的符号，得到的新数列{an}称为数列{An}的一个生成数列．如仅改变数列1，2，3，4，5的第二、三项的符号可以得到一个生成数列1，-2，-3，4，5．已知数列{an}为数列{
}(n∈N*)的生成数列，Sn为数列{an}的前n项和．
（1）写出S3的所有可能值；
（2）若生成数列{an}的通项公式为an=
，k∈N，求Sn；
（3）用数学归纳法证明：对于给定的n∈N*，Sn的所有可能值组成的集合为：{x|x=
，m∈N*，m≤2n-1}．
查看习题详情和答案>>
| 1 |
| 2n |
（1）写出S3的所有可能值；
（2）若生成数列{an}的通项公式为an=
|
（3）用数学归纳法证明：对于给定的n∈N*，Sn的所有可能值组成的集合为：{x|x=
| 2m-1 |
| 2n |
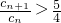的正整数n的个数；
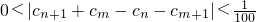成立．