摘要：计算焦点弦长可利用上面的焦半径公式. 一般地.若斜率为k的直线被圆锥曲线所截得的弦为AB. A.B两点分别为A(x1.y1).B(x2,y2).则弦长 ,这里体现了解析几何“设而不求 的解题思想,
网址：http://m.1010jiajiao.com/timu_id_4428747[举报]
已知椭圆C：
+
=1（a＞b＞0）的左顶点和右焦点分别为A，F，右准线为直线m，圆D：x2+y2-6y-4=0．
（1）若点A在圆D上，且椭圆C的离心率为
，求椭圆C的方程；
（2）若直线m上存在点Q，使△AFQ为等腰三角形，求椭圆C的离心率的取值范围；
（3）若点P在（1）中的椭圆C上，且过点P可作圆D的两条切线，切点分别为M、N，求弦长MN的取值范围． 查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
（1）若点A在圆D上，且椭圆C的离心率为
| ||
| 2 |
（2）若直线m上存在点Q，使△AFQ为等腰三角形，求椭圆C的离心率的取值范围；
（3）若点P在（1）中的椭圆C上，且过点P可作圆D的两条切线，切点分别为M、N，求弦长MN的取值范围． 查看习题详情和答案>>
已知椭圆
（a＞b＞0）的左顶点和右焦点分别为A，F，右准线为直线m，圆D：x2+y2-6y-4=0．
（1）若点A在圆D上，且椭圆C的离心率为
，求椭圆C的方程；
（2）若直线m上存在点Q，使△AFQ为等腰三角形，求椭圆C的离心率的取值范围；
（3）若点P在（1）中的椭圆C上，且过点P可作圆D的两条切线，切点分别为M、N，求弦长MN的取值范围．
查看习题详情和答案>>
（本题满分16分）
已知椭圆
的左顶点和右焦点分别为
，右准线为直线
，圆D：
．
（1）若点
在圆D上，且椭圆
的离心率为
，求椭圆C的方程；
（2）若直线上存在点Q，使
为等腰三角形，求椭圆C的离心率的取值范围；
（3）若点
在（1）中的椭圆C上，且过点P可作圆D的两条切线，切点分别为M、N，求弦长MN的取值范围．
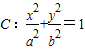（a＞b＞0）的左顶点和右焦点分别为A，F，右准线为直线m，圆D：x2+y2-6y-4=0．
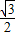，求椭圆C的方程；