摘要:13.如图5所示.两根光滑的金属导轨平行放置在绝缘斜面上.导轨的下方接有电阻R.导轨的电阻不计.斜面所在的空间有竖直向下的匀强磁场.质量为m.电阻不计的金属导体棒放在导轨上的ab位置.经过一段时间.导体棒从ab位置由静止开始自由运动到导轨上的cd位置.在此过程中.下列说法正确的是( ) A.导体棒在运动过程中机械能守恒 B.重力所做的功等于导体棒的动能增量 C.导体棒克服安培力所做的功等于电阻R上产生的热量 D.作用在导体棒上的合力所做的功等于导体棒的机械能的增量 第 Ⅱ卷
网址:http://m.1010jiajiao.com/timu_id_4427018[举报]
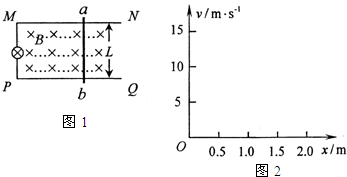 如图1所示,两根光滑的长直金属导轨 MN、PQ平行置于同一水平面内,导轨间距L=0.2m,导轨左端接有“0.8V,0.8W’’的小灯泡,导轨处于磁感应强度为B=1T、方向竖直向下的匀强磁场中.长度也为L的金属导体棒ab垂直于导轨放置,导轨与导体棒每米长度的电阻均为R0=0.5Ω,其余导线电阻不计.今使导体棒在外力作用下与导轨良好接触向右滑动产生电动势,使小灯泡能持续正常发光.
如图1所示,两根光滑的长直金属导轨 MN、PQ平行置于同一水平面内,导轨间距L=0.2m,导轨左端接有“0.8V,0.8W’’的小灯泡,导轨处于磁感应强度为B=1T、方向竖直向下的匀强磁场中.长度也为L的金属导体棒ab垂直于导轨放置,导轨与导体棒每米长度的电阻均为R0=0.5Ω,其余导线电阻不计.今使导体棒在外力作用下与导轨良好接触向右滑动产生电动势,使小灯泡能持续正常发光.(1)写出ab的速度v与它到左端MP的距离x的关系式,并求导体棒的最小速度vmin;
(2)根据v与x的关系式(图2),计算出与表中x各值对应的v的数值填入表中,然后画出v-x图线.
| x/m | 0 | 0.5 | 1 | 1.5 | 2 |
| v/ms-1 |
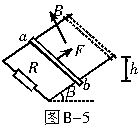
.两根光滑的金属导轨,平行放置在倾角为θ的斜面上,导轨的左端接有一电阻R,导轨自身的电阻可忽略不计,斜面处在一个匀强磁场中,磁场方向垂直于斜面向上.质量为m、电阻可忽略不计的金属棒ab,在沿着斜面、与棒垂直的恒力F作用下沿导轨匀速上滑,并上升高度为h.如图B-5所示,在这个过程中( )
A.作用于金属棒上的各力合力所做的功等于零
B.作用于金属棒上的各力合力所做的功等于mgh与电阻R上产生的焦耳热之和
C.恒力F与安培力的合力所做的功等于零
D.恒力F与重力的合力所做的功等于零
如图甲所示,两根足够长、电阻不计的光滑平行金属导轨相距为L1=1m,导轨平面与水平面成θ=30°角,上端连接阻值R=1.5Ω的电阻;质量为m=0.2kg、阻值r=0.5Ω的匀质金属棒ab放在两导轨上,距离导轨最上端为L2=4m,棒与导轨垂直并保持良好接触.整个装置处于一匀强磁场中,该匀强磁场方向与导轨平面垂直,磁感应强度大小随时间变化的情况如图乙所示.(g=10m/s2)
(1)保持ab棒静止,在0~4s内,通过金属棒ab的电流多大?方向如何?
(2)为了保持ab棒静止,需要在棒的中点施加了一平行于导轨平面的外力F,求当t=2s时,外力F的大小和方向;
(3)5s后,撤去外力F,金属棒将由静止开始下滑,这时用电压传感器将R两端的电压即时采集并输入计算机,在显示器显示的电压达到某一恒定值后,记下该时刻棒的位置,测出该位置与棒初始位置相距2.4m,求金属棒此时的速度及下滑到该位置的过程中在电阻R上产生的焦耳热.
查看习题详情和答案>>
(1)保持ab棒静止,在0~4s内,通过金属棒ab的电流多大?方向如何?
(2)为了保持ab棒静止,需要在棒的中点施加了一平行于导轨平面的外力F,求当t=2s时,外力F的大小和方向;
(3)5s后,撤去外力F,金属棒将由静止开始下滑,这时用电压传感器将R两端的电压即时采集并输入计算机,在显示器显示的电压达到某一恒定值后,记下该时刻棒的位置,测出该位置与棒初始位置相距2.4m,求金属棒此时的速度及下滑到该位置的过程中在电阻R上产生的焦耳热.

如图甲所示,两根足够长的光滑平行金属导轨相距l=0.4 m,导轨平面与水平面成θ=30°角,下端通过导线连接阻值R=0.5Ω的电阻.金属棒ab阻值r=0.3Ω,质量m=0.2kg,放在两导轨上,与导轨垂直并保持良好接触.其余部分电阻不计,整个装置处于垂直导轨平面向上的匀强磁场中.取g=10 m/s2.

(1)若磁场是均匀增大的匀强磁场,在开始计时即t=0时刻磁感应强度B0=2.0T,为保持金属棒静止,作用在金属棒上平行斜面向上的外力F随时间t变化的规律如图乙所示,求磁感应强度B随时间t变化的关系.
(2)若磁场是磁感应强度大小恒为B1的匀强磁场,通过额定功率P=10W的小电动机对金属棒施加平行斜面向上的牵引力,使其从静止开始沿导轨做匀加速度直线运动,经过
s电动机达到额定功率,此后电动机功率保持不变,金属棒运动的v-t图象如图丙所示.试求磁感应强度B1的大小和小电动机刚达到额定功率时金属棒的速度v1的大小?
查看习题详情和答案>>

(1)若磁场是均匀增大的匀强磁场,在开始计时即t=0时刻磁感应强度B0=2.0T,为保持金属棒静止,作用在金属棒上平行斜面向上的外力F随时间t变化的规律如图乙所示,求磁感应强度B随时间t变化的关系.
(2)若磁场是磁感应强度大小恒为B1的匀强磁场,通过额定功率P=10W的小电动机对金属棒施加平行斜面向上的牵引力,使其从静止开始沿导轨做匀加速度直线运动,经过
| 8 | 7 |
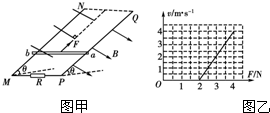 如图甲所示,两根足够长的光滑直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上,两导轨间距为L.M、P两点间接有阻值为R的电阻.一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直.整套装置处于磁感应强度为B的匀强磁场中,磁场方向垂直斜面向下.导轨和金属杆的电阻可忽略.用与导轨平行且向上的恒定拉力F作用在金属杆上,金属杆ab沿导轨向上运动,最终将做匀速运动.当改变拉力F的大小时,相对应的匀速运动速度v也会改变,v和F的关系如图乙所示.
如图甲所示,两根足够长的光滑直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上,两导轨间距为L.M、P两点间接有阻值为R的电阻.一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直.整套装置处于磁感应强度为B的匀强磁场中,磁场方向垂直斜面向下.导轨和金属杆的电阻可忽略.用与导轨平行且向上的恒定拉力F作用在金属杆上,金属杆ab沿导轨向上运动,最终将做匀速运动.当改变拉力F的大小时,相对应的匀速运动速度v也会改变,v和F的关系如图乙所示.(1)金属杆ab在匀速运动之前做什么运动?
(2)若m=0.25kg,L=0.5m,R=0.5Ω,取重力加速度g=10m/s2,试求磁感应强度B的大小及θ角的正弦值sin θ.